Use o Método de Newton para aproximar todos os valores reais de que satisfazem a equação dada para o valor de indicado.
Passo 1
Fala aí!! Tudo joia?
Olha só, a questão quer o valor da equação para . Então a primeira coisa que a gente faz é jogar esse valor no lugar de na expressão:
Agora o nosso trabalho é achar as raízes dessa equação. Aí é que entra o Método de Newton...
Passo 2
Se liga nesse gráfico pra ver as raízes:
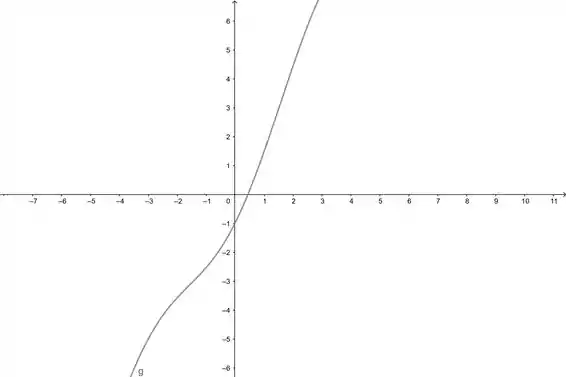
Passo 3
Para usar o método de Newton, a gente faz:
(aqui tá em , mas nossa função é em , não muda nada ok?)
Vamos precisar derivar:
E o nosso . Jogando na fórmula:
Show de bola! O valor de aproximado que satisfaz aquela equação lá é esse😉