Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.8 - Ex. 35
- Use o método de Newton para encontrar os números críticos da função com precisão de três casas decimais.
- Encontre o valor mínimo absoluto de com precisão de quatro casas decimais.
Passo 1
Fala aí, bora para mais uma?
Nessa questão temos a função que é:
E queremos encontrar o números críticos dessa função usando o método de Newton.
O que vai acontecer é que ao derivar essa função teremos uma função de quinto grau.
Para encontrar os números críticos (que são os pontos onde a derivada se anula), teremos que encontrar as raízes da derivada
E para isso vamos usar o método de Newton.
Basicamente, nós começamos com um chute inicial para essa raiz.
E para encontrar o próximo valor, faremos a seguinte iteração:
Como a função que queremos encontrar a raíz já é a derivada de , o m��todo de newton na realidade vai ficar escrito da seguinte forma:
E assim encontraremos os valores de onde
Dessa forma, repare que vamos precisar também encontrar a segunda derivada dessa função.
Depois vamos encontrar o valor mínimo absoluto com precisão de três casas decimais. Para isso, podemos substituir os números críticos na função e ver em qual caso teremos o menor valor, esse será o mínimo absoluto da função.
Passo 2
Para achar a derivada de vamos usar algumas regras de derivação, o da função constante e do polinômio:
Vamos calcular e :
Agora a segunda derivada.
Passo 3
Pronto, agora que temos e é só jogar na fórmula de Newton:
A questão não nos indicou quais são bons valores para chutes iniciais.
Dessa forma, não tem jeito, eu vou dar uma “roubadinha” e plotar o gráfico da para ver quais pontos ela possui raíz.
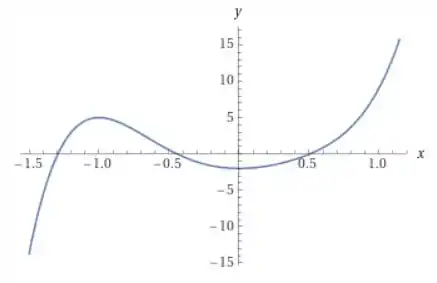
Parece que ela possui raízes em .
Vamos usar esses valores iniciais.
Passo 4
Primeiro para :
Como queremos uma precisão de três casas decimais, vamos continuar usando o método de Newton até o valor de deixar de variar, vamos lá:
Mais uma vez, agora com :
Pronto, o valor não varia mais, então a raiz é .
Passo 5
Agora com , vamos lá:
Como queremos uma precisão de oito casas decimais, vamos continuar usando o método de Newton até o valor de deixar de variar, vamos lá:
Mais uma vez, agora com :
Ainda está variando, vamos agora com :
Pronto, o valor não varia mais, então a raiz é .
Passo 6
Agora com , sei que é cansativo mas vamos lá:
Como queremos uma precisão de oito casas decimais, vamos continuar usando o método de Newton até o valor de deixar de variar, vamos lá:
Mais uma vez, agora com :
Pronto, o valor não varia mais, então a raiz é .
Passo 7
Temos dois pontos críticos quando muda de negativo para positivo (pontos de mínimo), e , então muda de decrescente para crescente, vamos então achar os desses dois valores e ver qual o menor:
Então, é o valor mínimo absoluto.
Resposta
(a)As raizes da equação são , e .
(b) é o valor mínimo absoluto