Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.Revisão - Ex. 5

Nos exercícios de 1 a 12, ache os extremos absolutos da função dada no intervalo indicado, se houver algum, e ache os valores de x nos quais os extremos absolutos ocorrem. Faça um esboço do gráfico da função no intervalo.

Passo 1

Seja f x = 9 - x 2 .   Como o domínio da função é [-2,3], temos que x 2 ≤ 9 . Logo, 9 - x 2 ≥ 0 no domínio indicado. Então é a mesma coisa que trabalharmos com a função F x = 9 - x 2 . As raízes de F(x) são x = ± 3

Passo 2

Calculando f ' ( x ) , teremos:

f ' x = - 2 x

Vejamos que a raiz de f ' ( x ) é 0 e que se:

x < 0 ,   f ' x > 0 x > 0 ,   f ' x < 0

Passo 3

Calculando agora f ' ' x :

f ' ' x = - 2

Dessa forma, temos que a função f é sempre côncava para baixo.

Passo 4

Passo 5

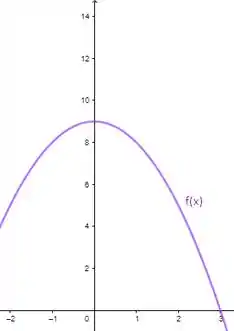
Utilizando esses dados e marcando alguns pontos, teremos o gráfico abaixo:

Passo 6

Vejamos que, verificando os pontos extremos do domínio, f - 2 = 5   e   f 3 = 0 . Com isso, temos que 9 é um máximo absoluto. Além disso, f 3 = 0   é um ponto de mínimo absoluto.

Resposta

Gráfico:

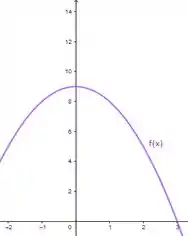
E os valores de máximo e mínimo absolutos da função são, respectivamente, 9   q u a n d o   x = 0   e   0   q u a n d o   x = 3 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre os valores máximo e mínimo absolutos de f nos intervalos fechados dados e indique onde ocorrem esses valores8. f x = 8 x - x 2 ; [ 0,6 ]
Encontre os valores máximo e mínimo absolutos, se houver, nos intervalos dados e indique onde esses valores ocorrem.21. f x = x 2 - x - 2 ; ( - ∞ , + ∞ )
Encontre os valores máximo e mínimo absolutos de f nos intervalos fechados dados e indique onde ocorrem esses valores9. f x = x - 2 3 ; [ 1 , 4 ]
37-50 Use qualquer método para encontrar os extremos da função f .45- f x = l n ⁡ ( 2 + x 2 )
37-50 Use qualquer método para encontrar os extremos da função f .43- f x = x + 3 x - 2