Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.8 - Ex. 28
Use o método de Newton para encontrar todas as soluções da equação correta para oito casas decimais. Comece desenhando um gráfico para aproximações iniciais.
Passo 1
Para fazer o que o enunciado pede, vamos ter que usar a seguinte fórmula do método de Newton.
Mas temos que passar nossa equação para forma de função, isso é de boa, basta jogar todo mundo para o mesmo lado, então:
Mas se você reparar precisaremos de um inicial, um no caso, e como o enunciado não fornece, temos que escolher um. Vamos escolher a parti de um certo método, vamos comparar os gráficos das duas funções presentes na equação, que são e e escolher o mais próximo da intercessão dos gráficos na parte positiva, abaixo temos esses gráficos.
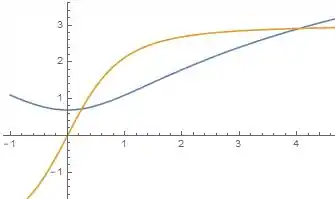
Se você reparar, nossos gráficos se interceptam duas vezes, logo teremos duas raízes os pontos bons que podemos escolher é e , já que eles estão perto das intercessões.
Você pode estar se perguntando, quando devo parar de fazer conta? Bem quando encontrarmos dois valores consecutivos iguais até a sexta casa decimal, que é a precisão pedida no enunciado, está na hora de parar e assim o primeiro na sequência dos repetidos é a nossa raiz.
Passo 2
Antes de começar a fazer conta, temos que escrever nossa equação na forma de função, então:
E agora derivar essa função para usar na fórmula mostrada em .
Agora partimos para fórmula.
Passo 3
Vamos então usar a bendita fórmula, primeiro para .
Que negócio feio, mas fazer o que?
Então:
Como , logo nossa raiz é .
Passo 4
Vamos então usar a bendita fórmula, agora para .
Que negócio feio, mas fazer o que?
Então:
Como , logo nossa raiz é .