Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.8 - Ex. 23

Use o método de Newton para encontrar todas as soluções da equação correta para oito casas decimais. Comece desenhando um gráfico para aproximações iniciais.

23 .   - 2 x 7 - 5 x 4 + 9 x 3 + 5 = 0

Passo 1

Fala aí! tudo certinho?

Nesse problema foi dada a equação

- 2 x 7 - 5 x 4 + 9 x 3 + 5 = 0

E nosso objetivo é obter as raízes dessa equação usando o método de Newton e usando seu gráfico para estimar os chutes iniciais.

Lembra como fazemos isso?

Para fazer o que o enunciado pede, vamos ter que usar a seguinte fórmula do método de Newton.

x n + 1 = x n - f ( x n ) f ' ( x n )

Onde f x é obtida como

f x = - 2 x 7 - 5 x 4 + 9 x 3 + 5

Com isso, montamos a equação do método a partir de f , f ' e de um chute inicial x 1 e repetimos os cálculos até encontrar dois valores iguais até a oitava casa decimal.

Show? Bora começar!

Passo 2

Primeiro vamos montar nossa formulinha, pra isso vamos calcular f ' ...

Pela regra da potência, temos

f ' x = - 2 7 x 7 - 1 - 5 4 x 4 - 1 + 9 3 x 3 - 1 + 5 0

f ' x = - 14 x 6 - 20 x 3 + 27 x 2

Com isso, nossa formulinha é dada por

x n + 1 = x n - f ( x n ) f ' ( x n )

x n + 1 = x n - - 2 x n 7 - 5 x n 4 + 9 x n 3 + 5 - 14 x n 6 - 20 x n 3 + 27 x n 2

Mas se você reparar precisaremos de um x n inicial, um x 0 no caso, e como o enunciado não fornece, temos que escolher um. Vamos escolher a partir do desenho do gráfico e usar o x 0 mais próximo da raiz.

Abaixo temos o gráfico da equação...

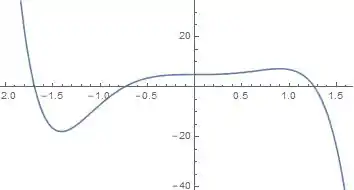
Se você reparar, nosso gráfico tem três raízes, então os pontos de melhor escolha são:

x 0 = - 1,7       x 0 = - 0,7       x 0 = 1,3

Bora começar!

Passo 3

Vamos então usar a bendita fórmula, primeiro para x 0 = - 1,7 .

Então para x 1 ...

x 1 = - 1,7 - - 2 ( - 1,7 ) 7 - 5 ( - 1,7 ) 4 + 9 ( - 1,7 ) 3 + 5 - 14 ( - 1,7 ) 6 - 20 ( - 1,7 ) 3 + 27 ( - 1,7 ) 2

x 1 = - 1,7 - 1,09023459 - 161,63596599

x 1 = - 1,69325499

Repetindo o cálculo para x 2 usando x 1

x 2 = - 1,69325499 - - 2 ( - 1,69325499 ) 7 - 5 ( - 1,69325499 ) 4 + 9 ( - 1,69325499 ) 3 + 5 - 14 ( - 1,69325499 ) 6 - 20 ( - 1,69325499 ) 3 + 27 ( - 1,69325499 ) 2

x 2 = - 1,69325499 - 0,02093080 - 155,45361714

x 2 = - 1,69312034

O resultado ainda não se repetiu, então vamos calcular novamente.

x 3 = - 1,69312034 - - 2 ( - 1,69312034 ) 7 - 5 ( - 1,69312034 ) 4 + 9 ( - 1,69312034 ) 3 + 5 - 14 ( - 1,69312034 ) 6 - 20 ( - 1,69312034 ) 3 + 27 ( - 1,69312034 ) 2

x 3 = - 1,69312034 - - 0,000007 - 155,33168771

x 3 = - 1,69312029

Mais uma vez...

x 4 = - 1,69312029 - - 2 ( - 1,69312029 ) 7 - 5 ( - 1,69312029 ) 4 + 9 ( - 1,69312029 ) 3 + 5 - 14 ( - 1,69312029 ) 6 - 20 ( - 1,69312029 ) 3 + 27 ( - 1,69312029 ) 2

x 4 = - 1,69312029 - - 0,0000005 - 155,33164245

x 4 = - 1,69312029

Como x 3 ≈ x 4 , logo nossa raiz é x 3 = - 1,69312029 .

Maravilha! Vamos para a segunda raiz!

Passo 4

Agora para x 0 = - 0,7 , vamos encontrar a próxima raiz...

x n + 1 = x n - - 2 x n 7 - 5 x n 4 + 9 x n 3 + 5 - 14 x n 6 - 20 x n 3 + 27 x n 2

Encontrando x 1

x 1 = - 0,7 - - 2 ( - 0,7 ) 7 - 5 ( - 0,7 ) 4 + 9 ( - 0,7 ) 3 + 5 - 14 ( - 0,7 ) 6 - 20 ( - 0,7 ) 3 + 27 ( - 0,7 ) 2

x 1 = - 0,7 - 0,87720860 18,442914

x 1 = - 0,74756344

Para x 2 , temos

x 2 = - 0,74756344 - - 2 ( - 0,74756344 ) 7 - 5 ( - 0,74756344 ) 4 + 9 ( - 0,74756344 ) 3 + 5 - 14 ( - 0,74756344 ) 6 - 20 ( - 0,74756344 ) 3 + 27 ( - 0,74756344 ) 2

x 2 = - 0,74756344 - - 0,06060712 21,00098999

x 2 = - 0,74467752

O resultado não se repetiu, então refazemos os cálculos...

x 3 = - 0,74467752 - - 2 ( - 0,74467752 ) 7 - 5 ( - 0,74467752 ) 4 + 9 ( - 0,74467752 ) 3 + 5 - 14 ( - 0,74467752 ) 6 - 20 ( - 0,74467752 ) 3 + 27 ( - 0,74467752 ) 2

x 3 = - 0,74467752 - - 0.00022596 20,84437485

x 3 = - 0,74466667

E mais uma vez...

x 4 = - 0,74466667 - - 2 ( - 0,74466667 ) 7 - 5 ( - 0,74466667 ) 4 + 9 ( - 0,74466667 ) 3 + 5 - 14 ( - 0,74466667 ) 6 - 20 ( - 0,74466667 ) 3 + 27 ( - 0,74466667 ) 2

x 4 = - 0,74466667 - - 0,0000001 20,84378625

x 4 = - 0,74466667

Como x 3 ≈ x 4 , logo nossa raiz é x 3 = - 0,74466667 .

Show! Encontramos mais uma!

Tranquilo até aqui?

Passo 5

Por último, vamos usar x 0 = 1,3 para encontrar a última raiz...

x n + 1 = x n - - 2 x n 7 - 5 x n 4 + 9 x n 3 + 5 - 14 x n 6 - 20 x n 3 + 27 x n 2

Obtendo x 1 ...

x 1 = 1,3 - - 2 ( 1,3 ) 7 - 5 ( 1,3 ) 4 + 9 ( 1,3 ) 3 + 5 - 14 ( 1,3 ) 6 - 20 ( 1,3 ) 3 + 27 ( 1,3 ) 2

x 1 = 1,3 - - 2,05720340 - 65,88532600

x 1 = 1,26877600

Agora x 2

x 2 = 1,26877600 - - 2 ( 1,26877600 ) 7 - 5 ( 1,26877600 ) 4 + 9 ( 1,26877600 ) 3 + 5 - 14 ( 1,26877600 ) 6 - 20 ( 1,26877600 ) 3 + 27 ( 1,26877600 ) 2

x 2 = 1,26877600 - - 0,16078912 - 55,78827513

x 2 = 1,26589386

Mais uma vez para x 3

x 3 = 1,26589386 - - 2 ( 1,26589386 ) 7 - 5 ( 1,26589386 ) 4 + 9 ( 1,26589386 ) 3 + 5 - 14 ( 1,26589386 ) 6 - 20 ( 1,26589386 ) 3 + 27 ( 1,26589386 ) 2

x 3 = 1,26589386 - - 0.00125848 - 54,91626629

x 3 = 1,26587094

Ainda não resultou em dois valores iguais... então vamos obter x 4

x 4 = 1,26587094 - - 2 ( 1,26587094 ) 7 - 5 ( 1,26587094 ) 4 + 9 ( 1,26587094 ) 3 + 5 - 14 ( 1,26587094 ) 6 - 20 ( 1,26587094 ) 3 + 27 ( 1,26587094 ) 2

x 4 = 1,26587094 - - 0,0000001 - 54,90937098

x 4 = 1,26587094

Como x 3 ≈ x 4 , logo nossa raiz é x 3 = 1,26587094 .

É isso! Encontramos todas as raízes de f !

O que achou? Responde Aí!

Resposta

x 3 = - 1,69312029

x 3 = - 0,74466667

x 3 = 1,26587094

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O volume de uma esfera é computado a partir do valor medido de seu raio. Estime o máximo erro percentual possível na medida se o erro percentual no volume deve ser mantido em não mais de ± 3 % ( V = 4
Use a diferencial d y para aproximar ∆ y de acordo com as mudanças de x. y = 3 x - 2 ; d ex = 2p a r ax = 2,03
Uma escada com 12m está apoiada em uma parede e faz um ângulo θ com o chão. Se o topo da escada está a uma altura de h m na parede, expresse h em termos de θ e então use d h para estimar a variação em
Um cubo de aço com 1 cm de lado é coberto com 0,01 cm de cobre. Use diferenciais para estimar o volume de cobre na cobertura. [sugestão: seha ∆ V a variação no volume do cubo).
A resitência elétrica R de um fio é dada por R = k r 2 , onde k é uma contante e r o raio do fio. Supondo que o raio do fio tenha um erro possível de ± 5 % , uso diferenciais para estimar o erro perce