Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 41
Represente graficamente a região entre as curvas e use a calculadora para encontrar a área até a quinta casa decimal.
Passo 1
Fala galerinha!
Temos as seguintes funções:
E o enunciado pede pra a gente usar uma calculadora gráfica pra nos ajudar a encontrar a área até a quinta casa decimal. Bora lá?!
A primeira coisa que fazemos é desenhar as curvas:
é a curva verde e é a parábola vermelha
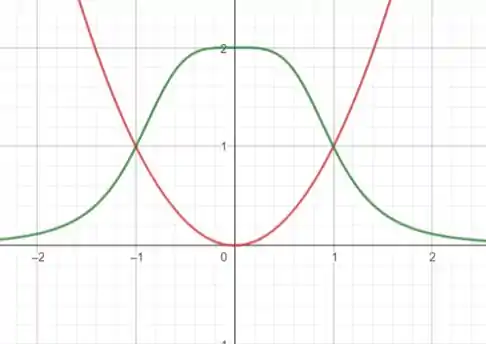
A área que queremos é essa intersecção!
Passo 2
Podemos ver que no intervalo de . Dessa forma podemos fazer:
Agora você vai usar o comando correspondente da sua calculadora gráfica para calcular essa integral! Vou deixar o valor aqui pra você conferir:
Resposta
Exercícios de Livros Relacionados
Determine o centro de massa do conjunto - 1 ≤ x ≤ 3 e 0 ≤ y ≤ x + 1 2 . (Sugestão: Resolva o problema no plano u , y , com u = x + 1 .)
Calcule o volume do sólido obtido pela rotação da região x 2 + 4 y 2 ≤ 1 , em torno da reta y = 1 .
Calcule o centro de massa da região dada: A=[ ( x , y )∈R ²/x ²+4 y ² ² ² ² ≤ 1 ,x ≥ 0ey ≥ 0 ]
Determine o centro de massa da região A dada.A = { ( x , y ) ∈ R 2 0 ≤ x ≤ 1 ,0 ≤ y ≤ x 3 }
a) Escreva, em coordenadas polares, a equação da elipse x 2 a 2 + y 2 b 2 = 1 tomando como pólo a origem e como eixo polar o semi-eixo O x .b) Escreva, em coordenadas polares, a equação da elipse x 2