Faça o gráfico das curvas nos Exercícios 27-42.
27.
Passo 1
Vamos usar o teste da segunda derivada para concavidade:
Para valores de maiores que , , ou seja, o gráfico de é côncavo para baixo.
Para valores de menores que 2, , ou seja, o gráfico de é côncavo para cima.
Em temos um ponto de inflexão.
Passo 2
Olhando a primeira derivada podemos identificar os máximos e mínimos locais:
Então ou
Como em o gráfico é côncavo para cima esse ponto é um mínimo local. E como em o gráfico é côncavo para baixo esse ponto é um máximo local.
Passo 3
Com essas informações já conseguimos fazer um bom esboço do gráfico:
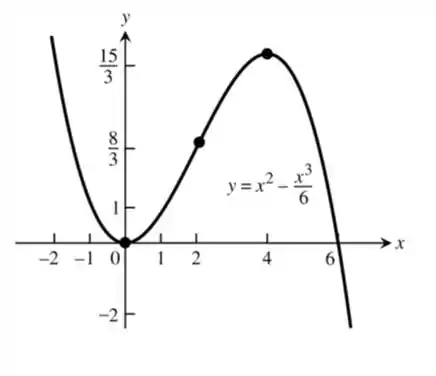
Resposta
Ei, a resposta está no passo a passo :)