Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.3 - Ex. 71
Uma curva de resposta à droga descreve o nível de medicamento na corrente sanguínea depois de uma droga ser administrada. Uma função onda é usada frequentemente para modelar a curva de resposta, refletindo uma oscilação inicial acentuada no nível da droga e então um declínio gradual. Se, para uma droga particular, , , e for medido em minutos, estime o tempo correspondente aos pontos de inflexão e explique seu significado. Se você tiver uma ferramenta gráfica, use-a para traçar a curva de resposta à droga.
Passo 1
Oii pessoal, show de bola??
“A loucura é como a gravidade, só precisa de um empurrãozinhooo...”
Bora resolve essa questãozinha comigo agora?!
A questão pede para estimar o tempo correspondente aos pontos de inflexão da curva de resposta à droga dada pela função
Onde:
é medido em minutos.
Além disso, a questão pede para explicar o significado dos pontos de inflexão e usar uma ferramenta gráfica para traçar a curva de resposta.
Os pontos de inflexão de uma função são os pontos onde a concavidade da curva muda. Isso ocorre quando a segunda derivada da função muda de sinal.
Passo 2
Para encontrar os pontos de inflexão, precisamos seguir estes passos:
1. Encontrar a primeira derivada da função
2. Encontrar a segunda derivada da função.
3. Resolver a equação da segunda derivada igual a zero para encontrar os possíveis pontos de inflexão.
4. Determinar se esses pontos são de fato pontos de inflexão verificando a mudança de sinal da segunda derivada.
A função dada é:
Substituindo os valores fornecidos:
Precisamos encontrar os pontos de inflexão para a função.
Passo 3
Encontrando a Primeira Derivada
Utilizamos a regra do produto para derivar:
Aplicando a regra do produto:
Passo 4
Encontrando a Segunda Derivada
Novamente, aplicamos a regra do produto para derivar
Portanto,
Passo 5
Para encontrar os pontos de inflexão, resolvemos a equação
Como
podemos simplificar para:
Fatoramos a equação:
Isso dá:
O primeiro termo , que não é um ponto de inflexão relevante para esta situação (início da administração da droga).
Passo 6
Para resolver a equação quadrática:
Usamos a fórmula quadrática
Calculando:
Então temos dois valores para
Passo 7
Os pontos de inflexão e indicam onde a concavidade da curva de resposta à droga muda.
Esses pontos podem indicar transições importantes na eficácia da droga no corpo, como a mudança de um aumento rápido para uma taxa de diminuição na concentração da droga.
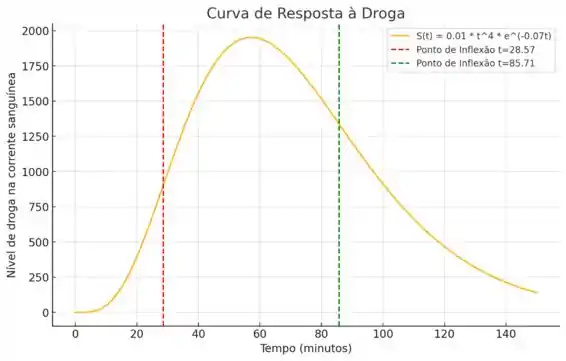
Aqui está o gráfico da curva de resposta à droga, mostrando o nível de medicamento na corrente sanguínea ao longo do tempo.
As linhas tracejadas vermelha e verde indicam os pontos de inflexão, em aproximadamente , respectivamente.
Esses pontos marcam onde a concavidade da curva muda, significando transições na taxa de aumento e diminuição do nível da droga no sangue.
“Faça seus medos terem medo de você”
