Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.3 - Ex. 53
Use projeção escalar para mostrar que a distância de um ponto à reta é
Use essa fórmula para determinar a distância do ponto à reta
Passo 1
Vamos ilustrar essa situação. Imagine que a gente tenha um vetor que seja perpendicular a nossa reta cuja equação é dada aí no enunciado.
Daí vamos imaginar também que temos nosso ponto , que não está na reta e queremos justamente saber a distancia dele até a reta, e também um ponto , que está na reta, assim:
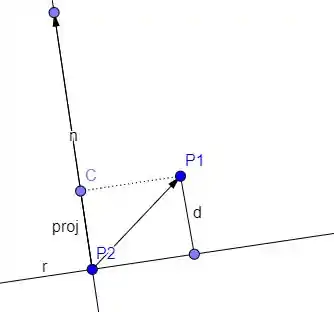
Se repararmos, a distancia do ponto até a reta é exatamente o valor da projeção escalar de sobre , que é dada por:
Passo 2
Vamos dar nome aos bois.
Vamos definir esse vetor :
Se , então, , assim
E vamos definir o vetor .
Passo 3
Agora podemos fazer o produto escalar:
E o módulo de :
Passo 4
Assim, temos
Da própria equação da reta, podemos tirar que
No ponto (que está na reta):
Substituindo isso ali em cima:
Ou seja,
Show de bola?!
Passo 5
Agora, para determinar a distância do ponto à reta é só substituir ali na formula: