Use qualquer método para encontrar os extremos relativos da função dada:

Vamos usar o teste da primeira derivada, calculando a derivada do quociente:

Agora, encontramos os zeros da primeira derivada:

A função fica indeterminada em .

Analisando o comportamento dos pontos em aplicados na primeira derivada, temos:

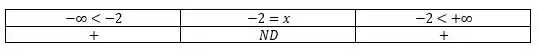
Como podemos observar, não há variação de intervalo, e portanto, não é ponto de máximo ou mínimo.