Use um recurso gráfico computacional para determinar o número de vezes que as curvas se intersectam; aplique, então, o Método de Newton, quando necessário, para aproximar as coordenadas de todas as intersecções.
Passo 1
E aí? Tudo joia? Vamos jogar esses gráficos no Geogebra pra ver essas interseções aí? Olha só:
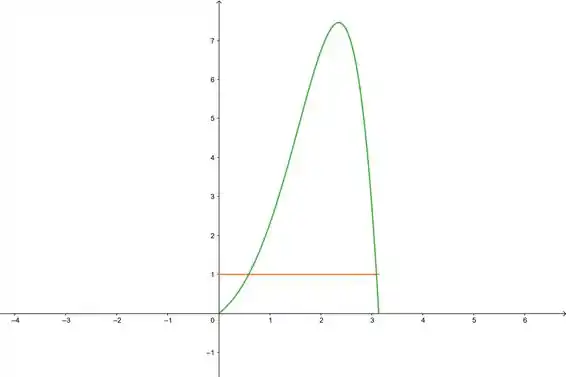
Como o gráfico nos mostra, são duas interseções! Vamos determinar onde elas são agora direitinho...
Passo 2
Pra achar a interseção a gente precisa fazer:
Pelo gráfico a gente vê que uma das interseções tá ali próxima de e a outra próxima de .
Vamos usar o Método de Newton pra aproximar esses valores então...
Passo 3
Pra usar o método de Newton, a gente precisa fazer:
Vamos derivar a função então:
Pra primeira interseção, vamos usar :
Tá tendo pouquinha variação já, então podemos parar por aqui e dizer que nossa interseção tá em aproximadamente
Passo 4
Falta a gente ver a outra interseção agora né? Vamos ver...
A gente pode chamar nosso e usar a mesma relação ali de cima:
Tá variando muito pouquinho, então já podemos dizer que nossa outra interseção está aproximadamente em .
E prontinho😉