Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.2 - Ex. 42
Use um recurso gráfico computacional para gerar algumas curvas de integrais representativas da função ao longo do intervalo
Passo 1
Primeiramente, vamos integrar a função dada:
A integral pode ser dada por:
Passo 2
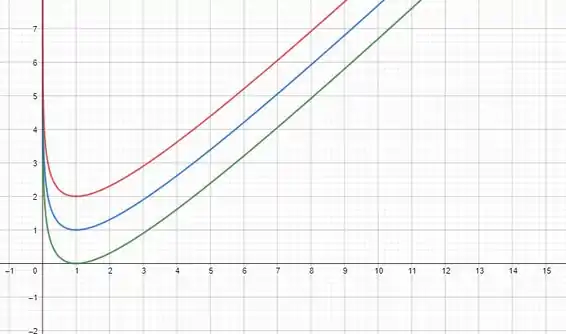
Agora que já temos o valor da função integrada, vamos plotar o gráfico em diferentes pontos, ao longo do invervalo. Alterando apenas a constante , quando está dentro do intervalo
Passo 3
Considerando os pontos iguais a :
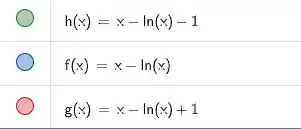
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
1-24. a) Use a Tabela de Integrais para calcular a integral. b) Se o leitor dispuses de um CAS, use-o para calcular a integral e, então, confirme que o resultado é equivalente ao que foi obtido em a).
1-24. a) Use a Tabela de Integrais para calcular a integral. b) Se o leitor dispuses de um CAS, use-o para calcular a integral e, então, confirme que o resultado é equivalente ao que foi obtido em a).
1-24. a) Use a Tabela de Integrais para calcular a integral. b) Se o leitor dispuses de um CAS, use-o para calcular a integral e, então, confirme que o resultado é equivalente ao que foi obtido em a).
1-24. a) Use a Tabela de Integrais para calcular a integral. b) Se o leitor dispuses de um CAS, use-o para calcular a integral e, então, confirme que o resultado é equivalente ao que foi obtido em a).
1-24. a) Use a Tabela de Integrais para calcular a integral. b) Se o leitor dispuses de um CAS, use-o para calcular a integral e, então, confirme que o resultado é equivalente ao que foi obtido em a).