Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.6 - Ex. 56

(a) Use um recurso gráfico computacional para gerar o gráfico de

f x = 1 100 ( x + 2 ) ( x + 1 ) ( x - 3 ) ( x - 5 )

e use o gráfico para fazer uma conjectura sobre o sinal da integral ∫ - 2 5 f x d x

(b) Verifique sua conjectura calculando a integral.

Passo 1

Pra esse polinômio, temos o gráfico:

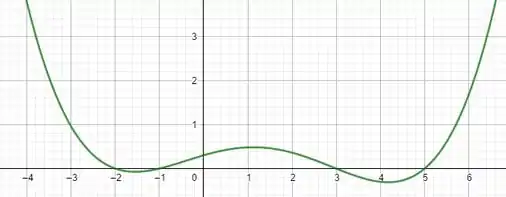
Podemos observar que nos pontos x = - 2 e x = 5 a função tem raízes. Caminhando no sentido de -2 até 5, vemos que entre -2 e-1 a função é negativa. O mesmo acontece entre 3 e 5.

Esses trechos vão contribuir pra redução da área total calculada pela integral. Ainda assim, a gente consegue ver que o trecho entre -1 e 3 a função é positiva e é um trecho notadamente maior que os anteriores.

“De olho”,a gente poderia dizer que a integral seria positiva.

Passo 2

(b)Calculamos:

∫ - 2 5 f x d x = 1 100 ∫ - 2 5 ( x + 2 ) ( x + 1 ) ( x - 3 ) ( x - 5 ) d x =

= 1 100 ∫ - 2 5 x 4 - 5 x 3 - 7 x 2 + 29 x + 30 d x =

= 1 100 x 5 5 - 5 x 4 4 - 7 x 3 3 + 29 x 2 2 + 30 x - 2 5

1 100 5 5 5 - 5 . 5 4 4 - 7 . 5 3 3 + 29 . 5 2 2 + 30 . 5 -

- 1 100 ( - 2 ) 5 5 - 5 - 2 4 4 - 7 - 2 3 3 + 29 ( - 2 ) 2 2 + 30 ( - 2 )

Resolvendo essas sentenças, temos no final:

∫ - 2 5 f x d x = 64,6 - ( - 9,7 ) 100 ≅ 0,74

De fato, concluímos que temos uma integral positiva!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

67 – a) Use um SAC para calcular: ∫ 0 π 2 s e n n x s e n n x + cos n ⁡ x d x onde n é um número inteiro positivo arbitrário. O seu SAC pode determinar o resultado?b) Em seguida, defina a integral qua
Mostre que a área da região no primeiro quadrante circundada pela curva y = 1 a cosh ⁡ a x , os eixos coordenados e a reta x = b é a mesma que a área de um retângulo de altura 1 a e comprimento s, ond
Assim como x = cos ⁡ u e y = s e nu são identificados com pontos ( x , y ) no círculo unitário, as funções x = cosh ⁡ u e y = s e n hu são identificadas com pontos ( x , y ) no ramo direito da hipérbo
Determine o centroide da região delimitada no primeiro quadrante pela curva y = 1 x + 1 e pela reta x = 3 .
Use a tabela de integrais e uma calculadora para determinar, com precisão de duas casas decimais, a área da superfície gerada pela rotação da curva y = x 2 ,- 1 ≤ x ≤ 1 , em torno do eixo x .