Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 7.3 - Ex. 86

Assim como x = cos ⁡ u e y = s e n   u são identificados com pontos ( x , y ) no círculo unitário, as funções x = cosh ⁡ u e y = s e n h   u são identificadas com pontos ( x , y ) no ramo direito da hipérbole unitária, x 2 + y 2 = 1 .

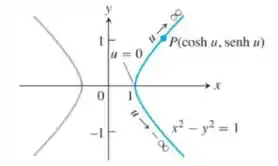
Uma vez que cosh 2 ⁡ u - s e n h 2   u = 1 , o ponto ( cosh ⁡ u ,   s e n h   u ) situa-se no ramo direito da hipérbole x 2 - y 2 = 1 para qualquer valor de u .

Outra analogia entre as funções hiperbólicas e circulares é que a variável umas coordenadas ( cosh ⁡ u ,   s e n h   u ) dos pontos do ramo direito da hipérbole x 2 - y 2 = 1 é o dobro da área do setor AOP ilustrado na figura a seguir. Para verificar por que isso ocorre, siga os passos a seguir.

  1. Mostre que a área A ( u ) do setor A O P é

    2. A u = 1 2 cosh ⁡ u   s e n h   u - ∫ 1 cosh ⁡ u x 2 - 1 d x

  2. Derive os dois lados da equação no item (a) com relação a u para mostrar que

    3. A ' u = 1 2

  3. Resolva essa última equação para A ( u ) . Qual é o valor de A ( 0 ) ? Qual o valor da constante de integração C na sua solução? Com C determinado, o que a sua solução diz sobre a relação entre u e A ( u ) ?

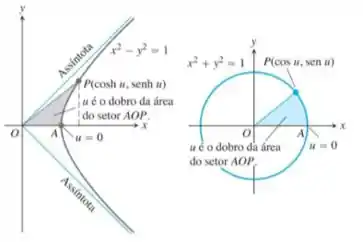
Uma das analogias entre as funções hiperbólicas e circulares é revelada por esses dois diagramas.

Passo 1

  1. Considere um ponto T localizado em ( cosh ⁡ u ,   0 ) . Temos então que a área do triângulo ∆ O T P é:

    2. A ∆ O T P = ( cosh ⁡ u   s e n h   u ) 2 = 1 2 cosh ⁡ u   s e n h   u

    A área do setor A O P é a área do triângulo menos a área sobre a curva y = x 2 - 1 no intervalo de 1 a cosh ⁡ u (dá uma olhada na figura do enunciado)... E como a área dessa curva é   A =   ∫ 1 cosh ⁡ u x 2 - 1   d x , a área do setor A O P é dada por:

    A A O P = 1 2 cosh ⁡ u   s e n h   u - ∫ 1 cosh ⁡ u x 2 - 1   d x  

    Passo 2

  2. Derivando em relação a u (a gente usa o Teorema Fundamental do Cálculo para derivar a integral) ficamos com:

    3. A ' A O P = 1 2 s e n h   u   s e n h   u + cosh ⁡ u   ( cosh ⁡ u ) - cosh 2 ⁡ u - 1 ( s e n h   u )

    (usando que s e n h 2 u = cosh 2 ⁡ u - 1 )

    A ' A O P = 1 2 s e n h 2 u + 1 2 cosh 2 ⁡ u - s e n h   u ( s e n h   u )

    A ' A O P = 1 2 s e n h 2 u + 1 2 cosh 2 ⁡ u - s e n h 2   u

    A ' A O P = 1 2 cosh 2 ⁡ u - 1 2 s e n h 2 u

    A ' A O P = 1 2 cosh 2 ⁡ u - s e n h 2 u = 1 2 1 = 1 2

    Como queríamos demonstrar.

    Passo 3

  3. Se A ' u = 1 2 , então A u = ∫ 1 2 d u = u 2 + C

Observe que se fizermos A ( 0 ) na equação do item (a), obtemos 0 como resultado, então A 0 = 0 . Daí podemos achar o valor da constante C fazendo:

A 0 = 0 2 + C = 0 → C = 0

Logo, A u = u 2 e u = 2 A ( u ) .

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a área da região sombreada.
Determine a área da região sombreada.
Determine a área da região sombreada.
Determine a área da região sombreada.
19 - Centroide de um triângulo situa-se na interseção das medianas do triângulo Você deve recordar que o ponto dentro de um triângulo que se situe a um terço do caminho de cada lado em direção ao vért