Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.7 - Ex. 37
Uma anuidade é uma sequência de pagamentos iguais que são pagos ou recebidos em intervalos regulares de tempo. Por exemplo, podemos querer depositar quantias iguais ao final de cada ano em uma poupança, a fim de acumular uma certa quantia em algum momento no futuro. Se, ao final de cada ano, forem acrescentados juros de i × 100% sobre o saldo da conta, então dizemos que a poupança paga i × 100% de juros, compostos anualmente. Pode-se mostrar que, se os depósitos de Q reais forem feitos ao final de cada ano, em uma poupança que paga i × 100% compostos anualmente, então, por ocasião do enésimo depósito e já depositados os juros do ano anterior, a quantia S(n) na poupança é dada pela fórmula
Suponha que queiramos depositar em uma poupança ao final de cada ano, com o objetivo de acumular $250.000 no 25° depósito. Qual é a taxa de juros compostos a ser paga para que possamos atingir essa meta? [Sugestão : Mostre que a taxa de juros i satisfaz a equação e resolva-a usando o Método de Newton.]
Passo 1
Fala aí!! Tudo joia?
Enunciado grande esse hein?! Hahaha...
Mas calma, vamos por partes... Primeiramente, vamos usar essa sugestão né?
Pelo enunciado, a gente tem que:
E aí simplificando, a gente tem:
E agora a gente que achar uma raiz pra essa função...
Passo 2
Aí a gente vai apelar pro método de Newton...
Para usar o método de Newton, a gente faz:
Vamos precisar derivar:
Olhando o gráfico a gente tem uma ideia de onde tá essa raiz:
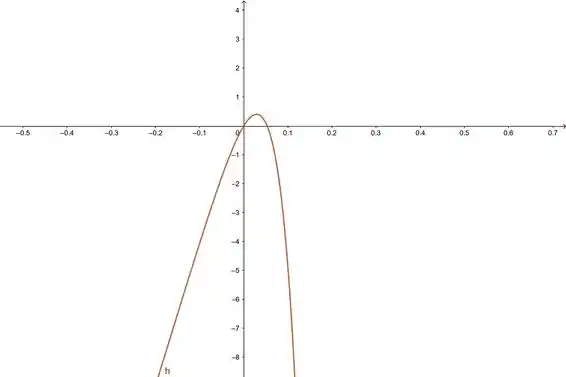
A gente vai usar pra jogar na fórmula e aproximar então. Bora lá!
Passo 3
Aplicando no método de Newton, temos:
Prontinho! A taxa de juros é de aproximadamente 😉