Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.7 - Ex. 35
Use o Método de Newton para aproximar todos os valores reais de que satisfazem a equação dada para o valor de indicado.
Passo 1
Fala aí!! Tudo joia?
Olha só, a questão quer o valor da equação para . Então a primeira coisa que a gente faz é jogar esse valor no lugar de na expressão:
Agora o nosso trabalho é achar as raízes dessa equação. Aí é que entra o Método de Newton...
Passo 2
Se liga nesse gráfico pra ver as raízes:
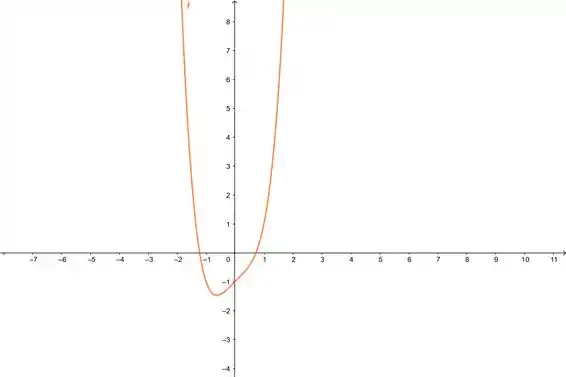
Então a gente tem uma raiz ali perto de e outra perto de . Show! Vamos pro método agora...
Passo 3
Para usar o método de Newton, a gente faz:
Vamos precisar derivar:
Vamos começar pela .
A gente joga na fórmula agora:
Beleza, pro primeiro ponto a gente pode usar essa aproximação de
Passo 4
Vamos ver o segundo ponto agora. Partimos de :
E belezinha! Vamos parar por aqui.
Os valores de que satisfazem a equação lá de cima são aproximadamente . 😸