Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.3 - Ex. 46
Use as cascas cilíndricas para encontrar o volume do sólido.
O toro sólido do Exercício 63 da Seção 6.2.
Passo 1
Eaee, belezinha?? Bom.. a questão quer que calculemos o volume do toro sólido abaixo:
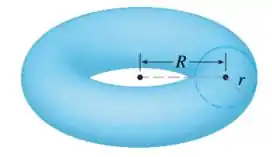
Para isso, a questão quer que utilizemos o método de cascas cilíndricas.
Mas que método é esse??
Bom... basicamente o volume de um sólido de rotação por esse método é dado por:
Agora vamos aplicar!! 😉
Passo 2
Então... o formato dessa figura é como se fosse um anel de guardanapo.
Por simetria, o volume desse anel obtido perfurando um buraco de raio através de uma esfera de raio é duas vezes o volume obtido pela rotação da área sobre o eixo e abaixo da curva (a equação da metade superior da seção transversal da esfera), entre e , sobre o eixo .
Assim, temos a seguinte figura:
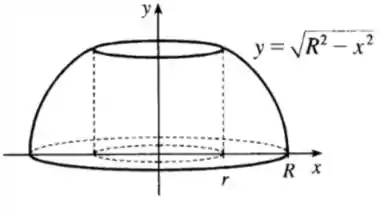
Passo 3
Sendo assim, nosso volume é dado por:
Passo 4
Usando o Teorema de Pitágoras, temos:
Assim, o volume do anel de guardanapo é:
Que é independente de e .
Entendeu direitinho?? Responde aee 😉