Enunciado
Cálculo Numérico - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.10 - Ex. 39
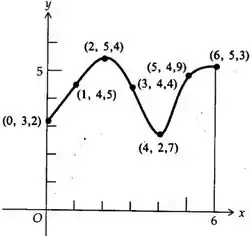
Use a regra de simpson para aproximar a área da região sombreada na figura.
Passo 1
Integração numéirca é um negócio que pode dar um pouquinho de trabalho se não organizarmos os dados que nós temos, porque as vezes pode ser um quantidade bem grande de dados. Então o primeiro passo é sempre fazer uma tabela organizando os dados que a questão nos deu:
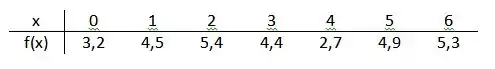
Passo 2
Com a tabela organizada, agora é só correr pro abraço: lembrar a fórmula e depois aplicar os valores.
Resposta
Exercícios de Livros Relacionados
Calcule a integral definida por dois métodos: a ) use a fórmula prismoidal dada no exercício 44 ; b ) use o segundo teorema fundamental do Cálculo ∫ 1 3 4 x 3 - 3 x 2 + 1 d x
Calcule a integral definida por dois métodos: a ) use a fórmula prismoidal dada no exercício 44 ; b ) use o segundo teorema fundamental do Cálculo ∫ - 2 2 x 3 + x 2 - 4 x - 2 d x
Calcule a integral definida por dois métodos: a ) use a fórmula prismoidal dada no exercício 44 ; b ) use o segundo teorema fundamental do Cálculo ∫ 2 6 2 x 3 - 2 x - 3 d x
A forma de um estacionamento é irregular e o comprimento do terredo de oeste a leste é 240m . No extremo oeste do terreno a largura é de 150m e no extremo leste é de 175m . Em 40,80,120,160 e 200m do
Ache a área da região limitada pelo laço da cura cuja equação é y 2 = 8 x 2 - x 5 . Calcule a integral definida pelas regras de Simpson com n = 8 e expresse o resultado com três casas decimais.