Use a série binomial para expandir a função como uma série de Maclaurin e para encontrar os três primeiros polinômios de Taylor, , e . Plote a função e esses polinômios de Taylor no intervalo de convergência

Se compararmos a nossa função:

Com a série binominal

Percebemos que no lugar do expoente aparece um , e no lugar de aparece , então a série da nossa função fica:

Agora, precisamos expandir esse termo binomial e descobrir o padrão.

O termo binomial é, para :

E para ,

Para o caso da nossa série, que temos termos , temos:

Começamos a mexer nisso reescrevendo os termos no numerador como frações de denominador :

Assim a gente pode juntar todos esse denominadores que estão sendo multiplicados com :

Juntando os denominadores e , e resolvendo as contas no numerador:

Agora a gente vai focar nesse termo . Caso , esse termo fica negativo. Então vamos seguir com essa condição, e reescrever ele como :

Agora a gente tem termos sendo multiplicados, todos com sinal de menos na frente. Se a gente juntar isso, fica :

Então, para , nosso padrão é:

Para , calculamos manualmente:

Sendo assim, a nossa série é

Substituindo os valores que encontramos:

Abrindo o expoente :

Podemos simplificar :

E esta é a nossa série!

Vamos usar o teste da razão para determinar o intervalo de convergência: para uma série , calculamos:

E a série vai convergir para .

Na nossa série,

Então,

Como , esses termos podem sair, e vamos juntar os termos parecidos para simplificar:

Calculando :

Resolvendo o limite:

Pelo teste da razão, a função converge para

Esse é o nosso intervalo de convergência.

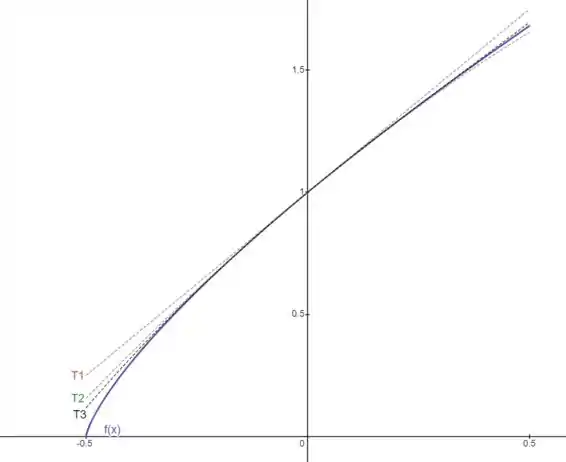
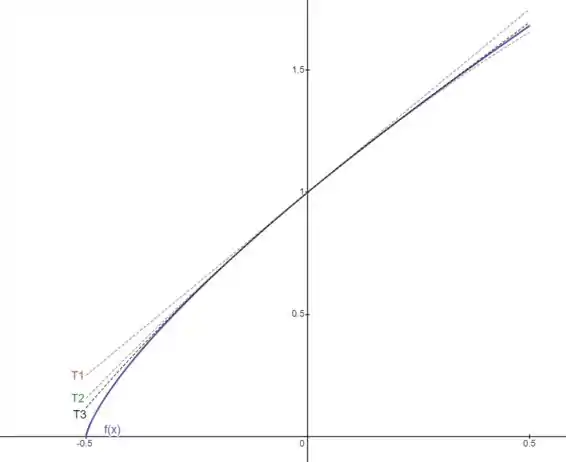
Como o intervalo de convergência é , vamos obter os plots em torno deste intervalo.

Relembrando que nossa série é:

Os polinômios que vamos plotar são:

Utilizando softwares para nos auxiliar, temos: