Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.6 - Ex. 19

Use um sistema algébrico computacional para fazer o gráfico de f e encontre f ' e f ' ' . Utilize os gráficos dessas derivadas para estimas os intervalos de crescimento, valores extremos, intervalos de concavidade e pontos de inflexão de f .

f x = sen 2 ⁡ x x 2 + 1 ,       0 ≤ x ≤ π / 3

Passo 1

Vamos derivar a função duas vezes usando um programa, obtendo f ' e f ' ' . Depois iremos olhar a primeira derivada pra estimar os intervalos de crescimento e decrescimento e os valores extremos. Finalmente, vamos estimar os intervalos de concavidade e os pontos de inflexão usando o gráfico de f ' ' .

Passo 2

Utilizando um programa, temos as derivadas de f :

f ' = sen ⁡ 2 x x 2 + 1 - x sen 2 ⁡ x x 2 + 1 3 / 2

f ' ' = 2 x 2 cos ⁡ 2 x - 2 x sen ⁡ 2 x + 2 cos ⁡ 2 x - sen 2 ⁡ x x 2 + 1 + 3 x 2 sen 2 ⁡ x x 2 + 1 5 / 2

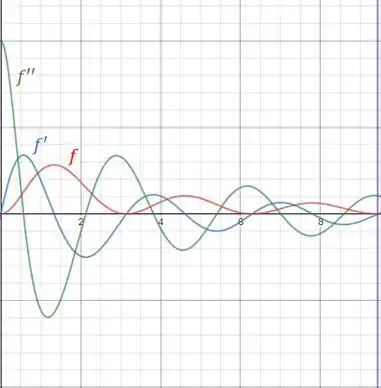
Os gráficos de f , f ' e f ' ' são então construídos:

Passo 3

Agora vamos usar o gráfico de f ' para estimar os intervalo de crescimento e decrescimento da função. A função f é crescente quando f ' é positivo e decrescente quando f ' é negativo. Olhando o gráfico, temos f ' positivo, e consequentemente função crescente, nos intervalos:

0 ,   1.33 , π ,   4.61   e   ( 2 π ,   7.79 )

E temos f ' negativo e função decrescente nos intervalos:

1.33 , π ,   4.61,2 π   e   ( 7.79 ,   3 π )

Os máximos e mínimos locais ocorrem quando f ' = 0 dentro do intervalo. Temos os máximos locais:

f 1.33 = 0.57       ( m á x i m o   a b s o l u t o )

f 4.61 = 0.21

E os mínimos locais:

f π = f 2 π = 0     ( m í n i m o   a b s o l u t o )

Passo 4

Pelo gráfico de f ' ' , estimamos os intervalos de concavidade e pontos de inflexão. Temos concavidade para cima quando f ' ' é positivo, e concavidade para baixo quando f ' ' é negativo. Os intervalos onde temos f ' ' positivo e concavidade para cima são:

0 ,   0.57 ,   2.13 ,   3.82 ,   5.4 ,   7   e   ( 8.58 ,   π )

E temos f ' ' negativo e concavidade pra cima nos intervalos:

0.57 ,   2.13 ,   3.82 ,   5.4   e   ( 7 ,   8.58 )

Os pontos de inflexão ocorrem quando a função muda de concavidade, ou seja, f ' ' muda de sinal. Isso ocorre quando f ' ' = 0 . Os pontos de inflexão são então:

0.57 ,   0.25 ,   2.13 ,   0.31 ,   3.82 ,   0.10 ,   5.4 ,   0.10 ,   7 ,   0.06   e   ( 8.58 ,   0.07 )

Resposta

Intervalos de crescimento: 0 ,   1.33 , π ,   4.61   e   ( 2 π ,   7.79 )

Intervalos de decrescimento: 1.33 , π ,   4.61,2 π   e   ( 7.79 ,   3 π )

Máximos locais: f 1.33 = 0.57   ( m á x i m o   a b s o l u t o ) e f 4.61 = 0.21

Mínimos locais: f π = f 2 π = 0   ( m í n i m o   a b s o l u t o )

Intervalos de concavidade para cima: 0 ,   0.57 ,   2.13 ,   3.82 ,   5.4 ,   7   e   ( 8.58 ,   π )

Intervalos de concavidade para baixo: 0.57 ,   2.13 ,   3.82 ,   5.4   e   ( 7 ,   8.58 )

Pontos de inflexão: 0.57 ,   0.25 ,   2.13 ,   0.31 ,   3.82 ,   0.10 ,   5.4 ,   0.10 ,   7 ,   0.06   e   ( 8.58 ,   0.07 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o roteiro desta seção para esboçar a curvay = x (ln (x))^2
Use o roteiro desta seção para esboçar a curvay = e^x - 3 e^(- x) - 4 x
33 (a)Se f ( x ) = x - ( 2 / x ) , encontre f ´ ( x ) . (b) Verifique se sua resposta em (a) foi razoável e comparando os gráficos de f e f ´
Trace ou copie o gráfico de f . (Suponha os eixos com a mesma escala.) Use o método do Exemplo 1 para esboçar o gráfico de f ' .
1-3.Use os gráficos dados para estimar o valor de cada derivada. Esboce então o gráfico de f ' .1.(a) f ' ( 1 ) ( b ) f ' ( 2 ) ( c ) f ' ( 3 ) ( d )f ' ( 4 )