Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.3 - Ex. 39

  1. Use a substituição trigonométrica pra verificar que

    2. ∫ 0 x a 2 - t 2   d t = 1 2 a 2 sin - 1 ⁡ x a + 1 2 x a 2 - x 2

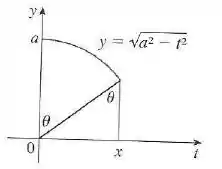
  2. Use a figura para dar interpretações geométricas de ambos os termos no lado direito da equação na parte (a)

Passo 1

  1. Primeiramente, não se desespera, calma e vamos trabalhar.

Pra resolver essa integral, vamos dizer que

t = a sin ⁡ θ

Diferenciando, temos que

d t = a cos ⁡ θ d θ

Calculando os novos limites de integração, temos

θ i n f e r i o r : 0 = a sin ⁡ θ ∴ θ = 0

θ s u p e r i o r : x = a sin ⁡ θ ∴ θ = sin - 1 ⁡ x a

Vamos dizer o seguinte, seja

a 2 - x 2

Temos que

a 2 - x 2 = a 2 - a 2 sin 2 ⁡ θ = a 2 1 - sin 2 ⁡ θ = a 2 cos 2 ⁡ θ = a cos ⁡ θ

Então

cos ⁡ θ = a 2 - x 2 a

Passo 2

  1. Substituindo na integral, temos que

    2. ∫ 0 x a 2 - t 2   d t = ∫ 0 sin - 1 ⁡ x a a 2 - a 2 sin 2 ⁡ θ a cos ⁡ θ d θ = ∫ 0 sin - 1 ⁡ x a a 2 1 - sin 2 ⁡ θ a cos ⁡ θ d θ = ∫ 0 sin - 1 ⁡ x a a 2 cos 2 ⁡ θ a cos ⁡ θ d θ = ∫ 0 sin - 1 ⁡ x a a 2 cos 2 ⁡ θ d θ = a 2 ∫ 0 sin - 1 ⁡ x a cos 2 ⁡ θ d θ = a 2 2 ∫ 0 sin - 1 ⁡ x a 1 + cos ⁡ 2 θ d θ = a 2 2 θ + 1 2 sin ⁡ 2 θ 0 sin - 1 ⁡ x a = a 2 2 θ + 1 2 sin ⁡ θ cos ⁡ θ 0 sin - 1 ⁡ x a = a 2 2 sin - 1 ⁡ x a + x a ⋅ a 2 - x 2 a = 1 2 a 2 sin - 1 ⁡ x a + 1 2 x a 2 - x 2

    Passo 3

  2. A integral ∫ 0 x a 2 - t 2 d t representa a área sob a curva y = a 2 - t 2 entre as linhas verticais t = 0 e t = x . A figura mostra que esta área consiste em uma região triangular e um setor do círculo t 2 + y 2 = a 2 . A região triangular tem base x e altura a 2 - x 2 , então sua área é 1 2 x a 2 - x 2 . O setor tem área 1 2 a 2 θ = 1 2 a 2 sin - 1 ⁡ ( x / a )

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule ∫ 1 x 1 + x 2 d x
Calcule ∫ 9 - x - 1 2 d x
Calcule ∫ x 2 1 - x 2 d x
Calcule ∫ 3 - 4 x 2 d x
Calcule ∫ 9 - 4 x 2 d x