Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.5 - Ex. 60
60. Se , use a tabela para estimar o valor de .
Passo 1
Oie, bora resolver mais uma?
A função é definida como
Isso significa que a função é uma composição de consigo mesma. Quando temos uma composição de funções, precisamos aplicar a função interna primeiro e, em seguida, aplicar a função externa. Neste caso, é obtido aplicando duas vezes.
Na tabela fornecida, procuramos os valores de quando Achamos que
Como a tabela não fornece diretamente os valores da derivada de podemos usar uma técnica de diferenciação numérica para estimar . Usamos a diferença dividida finita entre os valores de próximos a para isso.
Usando a regra da cadeia, sabemos que . Como já estimamos substituímos esse valor na expressão. Além disso, encontramos usando a mesma técnica de diferença dividida finita, pois também precisamos de no ponto onde
Substituímos os valores estimados de na expressão de para obter a estimativa final.
Ao seguir esses passos, podemos estimar usando os valores da tabela fornecida e técnicas de diferenciação numérica.
Passo 2
A regra da cadeia diz que quando temos uma “função dentro da outra”:
e queremos derivá-la, a gente faz a derivada da função de fora e multiplica pela derivada da função de dentro:
Só que nesse caso a função que está dentro é a mesma que está fora, então podemos escrever:
Como queremos , vamos substituir o por :
Sabemos, pela tabela, o valor de :
Passo 3
A derivada de uma função, em certo ponto, pode ser vista como sendo o coeficiente angular de uma reta tangente a função nesse ponto.
Nós não temos a função, mas podemos pegar dois pontos que estão próximos do que a gente deseja descobrir a derivada e traçar a reta que intercepta os dois:
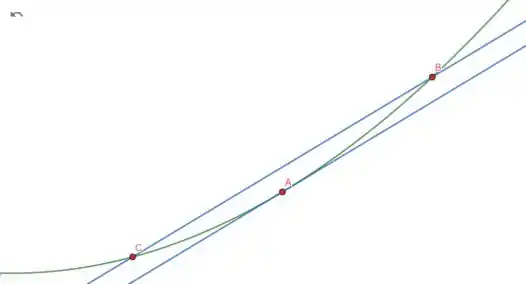
Perceba que essa reta vai ter uma inclinação parecida com a reta tangente no ponto A.
Então vamos pegar os valores dos lados dos ponto e do ponto 2 para a função :
A inclinação da reta é dada por:
Então podemos escrever que
Para a vamos fazer a mesma coisa:
Passo 4
Agora é só multiplicar os valores que encontramos: