Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.2 - Ex. 28
Use uma tabela de valores para estimar o valor de:
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu o seguinte limite:
Queremos elaborar uma tabela de valores para estimar o valor desse limite.
Mas como assim?
Bom... perceba que o limite diz , ou seja, “ tende a zero pelos números a sua direita”.
Em outras palavras, vamos colocar alguns valores de cada vez mais próximos de zero pelos números maiores que zero.
Com isso, vamos verificar o valor da função dentro do limite para cada citado. Lembrando que, analisando o limite, a função dentro dele é:
Agora bora lá!! 😉
Passo 2
Vamos escolher os seguintes valores de :
Assim, substituindo os valores presentes na tabela a seguir, obtemos os seguintes resultados para os valores da função :
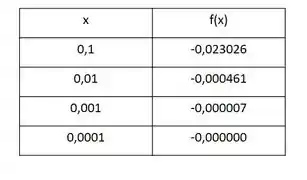
Logo, pela tabela, podemos perceber que a função fica cada vez mais próxima de zero quando tornamos cada vez mais próximo de zero.
Passo 3
É possível notar pelo gráfico que o valor da função se aproxima de zero conforme se aproxima de zero, veja:
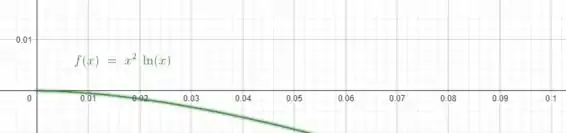
De fato, o gráfico confirma o que encontramos no passo 2. Sendo assim: