Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.11 - Ex. 29
Use o Teorema da Estimativa de Séries Alternadas ou a Desigualdade de Taylor para estimar a gama de valores de para os quais a aproximação dada tem precisão dentro do erro estabelecido. Verifique sua resposta graficamente.
Passo 1
Faala, pessoal!
Essa questão pede pra gente estimar pra que valores de que a aproximação:
Resulta num erro menor que .
E dá a opção de usarmos o Teorema da Estimativa de Série Alternadas, ou a Desigualdade de Taylor.
Como essa série é uma série alternada, vamos usar o teorema!
Primeiro, vamos encontrar a série que define o arco-tangente.
Já que:
Vamos escrever essa derivada como uma série, a partir dessa:
E depois integrar dos dois lados, pra achar a série do .
Depois que tivermos encontrado a série, vamos usar o Teorema da Estimativa de Série Alternadas. Ele diz que para uma série , se tivermos:
- , e
Então
Onde é o erro do polinômio que inclui até o -ésimo termo da série.
O que esse teorema diz é que, satisfeitas as condições, o erro vai ser menor do que o próximo termo da série (sem o sinal), que é o !
Por último, vamos plotar a função e o polinômio pra confirmar o que achamos.
Eu sei que parece muita coisa, mas vamos aos poucos que vai sair!!
Passo 2
Vamos começar então, achando a série do , sabendo que:
Vamos comparar isso com essa série:
Percebe que no lugar do , no nosso caso temos . Substituindo, temos que:
Passo 3
Só que isso é:
Integrando dos dois lados:
Como o é uma soma de infinitos termos, podemos colocar a integral pra dentro, que é o equivalente a abrirmos uma integral da soma numa soma de integrais:
E integramos:
Passo 4
Agora vamos aplicar o teorema.
Bom, nossa série pode ser aberta assim:
Antes de aplicar, temos que testar as condições do teorema. Nossa série é:
Então
(i)
Cancelando dos dois lados:
Percebe que esse termo da direita vai diminuindo conforme aumentamos o . Pra sermos conservadores, e garantir essa condição, vamos pegar :
Essa é a nossa primeira condição.
(ii)
Vamos usar L’Hospital (lembra que nossa variável do limite é , não ):
Esse limite só vai dar zero se:
Que é a mesma condição pra satisfazer (i).
Passo 5
Então estamos num universo que
Pelo teorema, o erro vai ser menor do que o próximo termo. Nosso polinômio inclui os três primeiros termos da série :
Então:
Queremos que isso seja menor que :
Então:
Percebe que esses valores de estão dentro do nosso universo
Então pra nesse intervalo, a aproximação tem erro menor que !
Passo 6
Pra ver isso graficamente, vamos plotar três funções:
Nós queremos que no intervalo de a função esteja entre e , porque isso quer dizer que ela vai ter uma diferença de no máximo pro valor real de .
Pra isso, vamos usar o Desmos pro desenho:
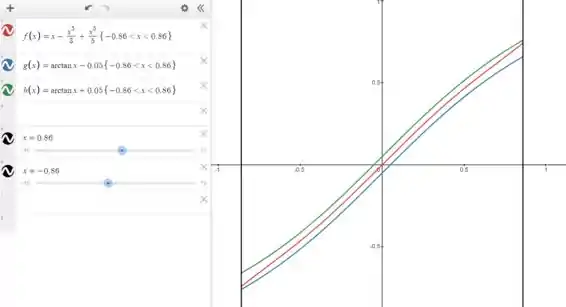
As retas em preto são os limites do intervalo que a gente ta interessado.
Percebe que a curva vermelha está entre as outras duas, que é exatamente o que a gente queria!!