Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.4 - Ex. 17
Use o Teorema de Green para achar o trabalho realizado pela força ao mover uma partícula da origem ao longo do eixo até, em seguida ao longo de um segmento de reta até , e então de volta à origem ao longo do eixo .
Passo 1
E aiii meu povo, beleza?
Nessa questão, devemos usar o Teorema de Green para achar o trabalho realizado por uma força ao mover uma partícula no plano .
Essa partícula se move da seguinte maneira: parte da origem ao longo do eixo até, em seguida ao longo de um segmento de reta até , e então de volta à origem ao longo do eixo .
E agora???
Nosso primeiro objetivo é entender a região . Conforme a trajetória da partícula, podemos concluir que:
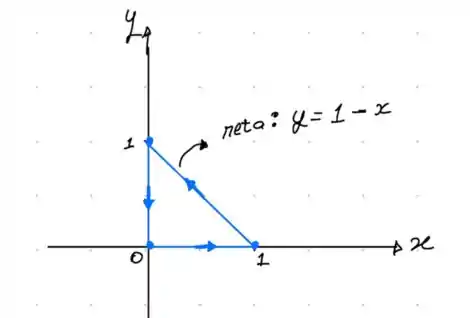
Olhando para a figura, podemos concluir que os intervalos de variação de x e y são:
Também sabemos que o trabalho dessa força pode ser expresso pela seguinte integral de linha:
Pelo Teorema de Green, podemos relacionar uma integral de linha em uma curva fechada como uma integral dupla de área. Desse jeito:
Onde, e são respectivamente no vetor :
Agora já podemos montar nossa integral e resolvê-la.
Vamos nessa!!!
Passo 2
Conforme a trajetória da partícula, conseguimos fazer o seguinte gráfico:
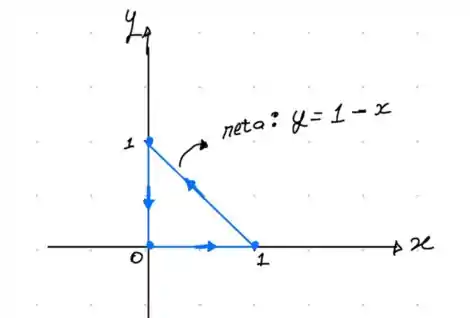
Olhando para a figura, podemos concluir que os intervalos de variação de x e y são:
Como a trajetória é no sentido anti-horário, isso implica que podemos aplicar o Teorema de Green.
Mas antes vamos lembrar que o trabalho da partícula ao longo dessa trajetória, pode ser expresso como:
Pelo teorema de Green temos que:
Onde, e são respectivamente no vetor :
Passo 3
Do enunciado sabemos que é:
Logo e são respectivamente:
Substituindo no Teorema de Green, temos:
Derivando e substituindo os intervalos de integração:
Temos:
Um ponto bem importante, sempre que um intervalo de integração depender de funções, ele deve ser integrado primeiro.
Assim, devemos integrar primeiro em .
Passo 4
Integrando em , vamos ter:
Aplicando os limites de integração, ficamos com:
Agora, integrando em temos:
Aplicando os limites de integração, tem-se:
Por fim, concluímos que aplicando o Teorema de Green obtemos como resposta: