Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.8 - Ex. 1b
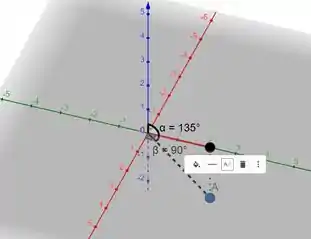
Marque o ponto cujas coordenadas esféricas são dadas. A seguir, encontre as coordenadas retangulares do ponto.
Passo 1
Fala, pessoal! Tudo certo?
A questão quer que a gente marque, ou seja, localize um ponto em coordenadas esféricas e depois pede para encontrarmos o equivalente desse ponto em coordenadas retangulares:
As relações entre coordenadas esféricas e coordenadas retangulares são dadas da seguinte forma:
Então, vamos precisar usar as equações acima para transformar nosso ponto em um ponto de coordenadas retangulares.
Vamos lá.
Passo 2
Vamos começar esboçando o ponto. Portanto,
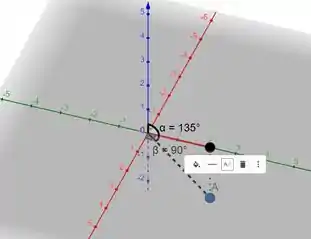
Em vermelho temos o eixo , em verde o e o eixo em azul.
Passo 3
Vamos resolver o nosso sistema agora. Portanto,
Para coordenadas retangulares, procuramos , ou seja:
Substituindo os valores de cada variável:
Temos:
Portanto, temos o ponto:
Resposta
