Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.8 - Ex. 12
-
Use o Teorema de Stokes para calcular , onde
e é a curva resultante do parabolóide hiperbólico e o cilindro , orientado no sentido anti-horário vista de cima.
-
Esboce o gráfico o plano e do cilindro com os domínios escolhidos, de modo que seja possível ver a curva e a superfície usada na letra (a);
-
Encontre as equações paramétricas para e as use para esboçar o gráfico de .
e é a curva resultante do parabolóide hiperbólico e o cilindro , orientado no sentido anti-horário vista de cima.
Passo 1
Fala ai galera galera, esse exercício nos pede bastante coisa. A primeira delas é calcular pelo teorema de Stokes, onde:
e é a curva resultante do parabolóide hiperbólico e o cilindro , orientado no sentido anti-horário vista de cima.
Pessoal, o Teorema de Stokes é dada por
Logo, iremos começar calculando o rotacional pela fórmula:
onde .
Beleza, o próximo passo é identificar a curva e a superfície S que a curva delimita. E vou dar um spoiler antes de começarmos, ta?
Se a superfície é da forma e é orientada para cima, podemos usar a seguinte fórmula
Sabemos que faz parte do plano e que é a projeção da superfície no plano .
Beleza, depois disso iremos transformar em coordenadas polares para facilitar a nossa vida , achar os limites e resolver a integral.
Na letra b ele pede para esboçar o gráfico o plano e do cilindro com os domínios escolhidos, de modo que seja possível ver a curva e a superfície usada na letra (a);Logo podemos achar as equações do parabolóide e do cilindro e colocar em um software como o Geogebra.
E a última coisa que ele nos pede é achar as equações paramétricas, mas pera lá, a gente já vai ter praticamente feito isso na letra (a) porém teremos que achar o valor de z.
Vamos começar !!!!!
Passo 2
Na letra (a), queremos o valor de , certo? Simbora calcular! Por definição,
Sabendo que:
onde .Temos:
Certo, então precisamos achar as derivadas parciais do jeito que mostra a fórmula.
Vamos começar por:
Assim:
e
Substituindo na fórmula do rotacional :
Passo 3
Agora vamos encontrar:
Assim:
e
Substituindo em:
Logo:
Passo 4
Por último vamos achar:
Assim:
e
Substituindo em :
Logo:
Opa , então nosso rotacional será:
Passo 5
Já achamos o rotacional, agora lembra que como achamos que a superfície é da forma orientada para cima, podemos usar a seguinte fórmula
Ou seja, agora precisamos achar quem é para multiplicarmos com o nosso rotacional.
Onde :
Sabemos que .Logo:
Assim:
Dessa forma:
Passo 6
Está quase acabando. Vamos passar aqui as variáveis para coordenadas cilíndricas, para facilitar nossa vida!
Sabemos que representa no plano uma circunferência de , e como vamos queremos toda a região do cilindro, nossos limites de integração serão:
e
Assim, substituindo na integral:
colocando em evidência e sabendo que
Assim:
Multiplicando :
Vamos lá que tá quase acabando!
Passo 7
Na letra (b) queremos o gráfico da interseção do plano e do cilindro, que resultam na curva . Assim,Sabemos que temos um cilindro e um parabolóide.
Logo:
Paraboloide é igual :
cilindro é igual :
Sabendo que:
e
Projetando o gráfico: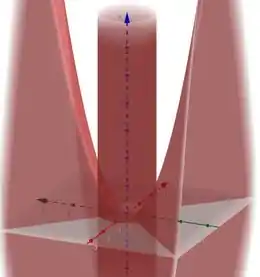
Passo 8
Na letra (c) nos é pedido uma parametrização para a curva .
A representação paramétrica do cilindro é:
A equação do parabolóide hiperbólico é .
Para os pontos no cilindro
Como
Portanto, a representação paramétrica da interseção entre o plano e o cilindro é:
Resposta
- ;
- .
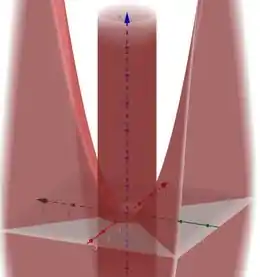