Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 11.1 - Ex. 5

5. Seja F ( x ,   y ,   z )   = ( 0,0 , x 3 ) e seja σ a superfície z = y + 4 com 1   ≤   x 2 + y 2 ≤   4 , com normal apontando para baixo. Calcule

∫ ∫ σ   ∇ × F → ⋅   n →   d S  

Passo 1

Vamos calcular pelo teorema de Stolkes

∫ ∫ σ   ∇ × F → ⋅   n →   d S =   ∫ γ F ⋅ d r

E nossa região projetando no plano XY é essa abaixo

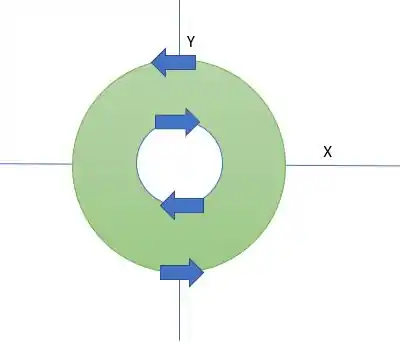
Como podemos ver pela equação

1   ≤   x 2 + y 2 ≤   4

Logo teremos que fazer uma composição de integral de contorno

∫ ∫ σ   ∇ × F → ⋅   n →   d S =   - ∫ γ 1 F ⋅ d r + ∫ γ 2 F ⋅ d r

Lembre-se que a circulação do contorno importa para o cálculo. Como queremos excluir o círculo interno, ele terá circulação contraria e sinal negativo na integral

Passo 2

Vamos parametrizar nossas curvas e calcular essa integral de linha. Nosso γ 1 pode ser escrito da seguinte forma

    γ 1 = cos ⁡ t ,   s e n   t ,   s e n   t + 4

γ 1 ' = - s e n   t , cos ⁡ t , cos ⁡ t

Assim

F   γ 1   t = 0,0 , cos 3 ⁡ t

E nossa curva γ 2 podemos parametrizar da seguinte forma

γ 2 = 2 cos ⁡ t ,   2 sin ⁡ t , 2 sin ⁡ t + 4

γ 2 ' = - 2 sin ⁡ t , 2 cos ⁡ t , 2 cos ⁡ t

E nossa função parametrizada fica

F   γ 2   t = 0,0 , 8 cos 3 ⁡ t

Passo 3

Vamos integral

∫ ∫ σ   ∇ × F → ⋅   n →   d S =   - ∫ γ 1 F ⋅ d r + ∫ γ 2 F ⋅ d r

=   - ∫ γ 1 F ( γ 1 t ) ⋅ ( γ ' 1 ) d t + ∫ γ 2 F ( γ 2 t ) ⋅ ( γ ' 2 ) d t

=   - ∫ 0 2 π 0,0 , cos 3 ⁡ t ⋅ - s e n   t , cos ⁡ t , cos ⁡ t d t + ∫ 0 2 π 0,0 , 8 cos 3 ⁡ t ⋅ - 2 sin ⁡ t , 2 cos ⁡ t , 2 cos ⁡ t d t

=   - ∫ 0 2 π cos 4 ⁡ t d t + ∫ 0 2 π 16 cos 4 ⁡ t d t

= 15 ∫ 0 2 π cos 4 ⁡ t d t

= 45 π 4

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

∫ ∫ σ   ∇ × F → ⋅   n →   d S =   45 π 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o Teorema de Stokes para calcular ∬ S ∇ → × F → ⋅ d S → . F → x , y , z = t g - 1 x 2 y z 2 i ^ + x 2 y j ^ + x 2 z 2 k ^ 0 ≤ x ≤ 2 ,o r i e n t a d on ad i r e ç ã od oe i x oxp o s i t i v o çã
Use o Teorema de Stokes para calcular ∬ S ∇ → × F → ⋅ d S → . F → x , y , z = e x y + e x z j ^ + x 2 z k ^ Sém e t a d ed oe l i p s o i d e4 x 2 + y 2 + 4 z 2 = 4 , é o r i e n t a d on ad i r e ç ã
Use o Teorema de Stokes para calcular ∮ C F → ⋅ d r → . Em cada caso, C é orientado no sentido anti-horário quando visto de cima. F → x , y , z = i ^ + x + y z j ^ + x y - z k ^ , C é o limite da part
Use o Teorema de Stokes para calcular ∫ C F .d r . Em cada caso, C é orientado no sentido anti-horário visto de cima.10- F x , y , z = x i + y j + x 2 + y 2 k , C é a fronteira da parte do paraboloide
Use o Teorema de Stokes para calcular ∫ ∫ S r o tF .d S 2- F x , y , z = y zi + x zj + x yk S é a parte do paraboloide z = 9 - x 2 - y 2 que está acima do plano z = 5 , com orientação para cima.