Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.7 - Ex. 11

Calcule a integral de superfície.

∬ x d S

S é a região triangular com vértices 1,0 , 0 , 0 , - 2,0   e   0,0 , 4 .

Passo 1

Notem que a região triangular descrita é parte de um plano. Como os vértices 1,0 , 0 ,   0 , - 2,0   e   ( 0,0 , 4 ) estão nos eixos, nós podemos escrever a equação do plano como:

x 1 + y - 2 + z 4 = 1

Multiplicando tudo por 4 ,

4 x - 2 y + z = 4 → z = 4 - 4 x + 2 y

Galera, para calcularmos essa integral de superfície, precisamos trabalhar inicialmente com as equações paramétricas. Sabemos que

f x , y , z = x

Qualquer superfície S com equação z = g ( x , y ) pode ser considerada uma superfície parametrizada com equações parametrizadas. Neste caso, a integral de superfície se torna:

∬ f x , y , z d S = ∬ f x , y , g x , y ∂ z ∂ x 2 + ∂ z ∂ y 2 + 1 d A

Precisamos achar as derivadas parciais de z . Assim,

∂ z ∂ x = - 4

∂ z ∂ y = 2

Escrevendo a expressão que fica dentro da integral:

f x , y , g x , y ∂ z ∂ x 2 + ∂ z ∂ y 2 + 1 = x 4 2 + 2 2 + 1

f x , y , g x , y ∂ z ∂ x 2 + ∂ z ∂ y 2 + 1 = x 21

Passo 2

Nós estamos interessados na área D que é a projeção da superfície no plano x y . Como x é interceptado em 1 e y em - 2 , os vértices do triângulo são 0,0 ,   1,0   e   ( 0 , - 2 ) .

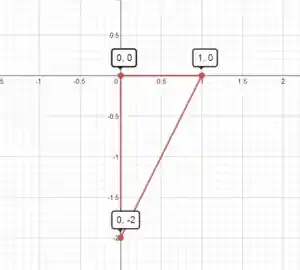
A equação da reta ligando os pontos 1,0   e   ( 0 , - 2 ) é dada por x 1 + y - 2 = 1 , que pode ser reescrita como y = 2 x - 2 . Logo, podemos definir a região como { ( x , y ) ∈ D   | 0 ≤ x ≤ 1 ,   2 x - 2 ≤ y ≤ 0 } .

Passo 3

Vamos agora substituir esses valores encontrados na integral!

∬ f x , y , z d S = 21 ∫ 0 1 ∫ 2 x - 2 0 x   d y d x

∬ f x , y , z d S = 21 ∫ 0 1 x y 2 x - 2 0 d x

∬ f x , y , z d S = 21 ∫ 0 1 - x ( 2 x - 2 ) d x = 21 ∫ 0 1 [ - 2 x 2 + 2 x ]   d x

Estamos quase lá!

∬ f x , y , z d S = 21 2 x 3 3 - x 2 0 1

∬ f x , y , z d S = 21 2 3 - 1

∬ f x , y , z d S = 21 3

Resposta

A integral é igual a

∬ f x , y , z d s = 21 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a área da parte da esfera x 2 + y 2 + z 2 = a 2 que está dentro do cilindro x 2 + y 2 = a x .
(a) Determine, mas não calcule, a integral dupla da área da superfície com as equações paramétricas x = au cos ⁡ v,y = bus e nv,z = u 2,0 ≤ u ≤ 2,0 ≤ v ≤ 2 π (b) Elimine os parâmetros para mostrar que
Calcule a integral de superfície. ∫ ∫ S( x 2 + y 2 + z 2 )d S S é a parte do cilindro y 2 + z 2 = 9 entre os planos z = 0 e z = 2 , juntamente com os discos do fundo e do topo
Calcule a integral de superfície. ∫ ∫ S1 + x 2 + y 2d S S é o helicoide com equação vetorial r u ,v = u cos ⁡ v i + us e nvj + vk, 0 ≤ u ≤ 1, 0 ≤ v ≤ π
Calcule a integral de superfície. ∫ ∫ Sy 2d S S é a parte da esfera x 2 + y 2 + z 2 = 4 que está dentro do cilindro x 2 + y 2 = 1 e acima do plano x y .