38. a) Use um recurso computacional para gerar o gráfico da função e, então, use o gráfico para fazer uma conjectura sobre o número e a localização de todas as descontinuidades.
b) Use o Teorema do Valor Intermediário para localizar aproximadamente todos os pontos de descontinuidade com duas casas decimais de precisão.
Passo 1
a)
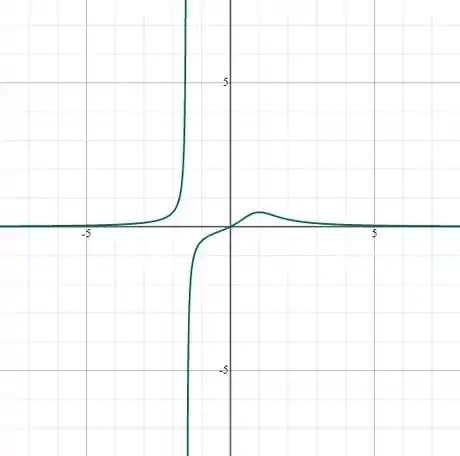
Olhando esse gráfico, ele aparenta ter um único ponto onde a função é descontinua, mas porque apenas um?
Lembre-se que os pontos onde a função provavelmente é descontínua são os pontos onde a função não está definida e como a função em questão é uma função racional, esse ponto provavelmente é uma das raízes de.
Como tem apenas uma raiz, nós poderiamos ter um ou nenhum ponto de descontinuidade.
Observando o gráfico, também é possivel obter a informação de que esse ponto de descontinuidade está entre no intervalo .
Passo 2
b) Bom, como vimos anteriormente, o ponto de descontinuidade com certeza é um ponto onde se anula, ou seja, em uma raiz desse polinômio. Então vamos fazer a análise dessa função para encontrar essa raiz.
Note que essa análise não poderia ser feita para, pois o teorema do valor intermadiario só pode ser aplicado para funções contínuas em um intervalo, e tem um ponto de descontinuidade em .
Como é contínua em e como então existe tal que .
Sabendo que a raiz está no intervalo , vamos tentar reduzir esse intervalo para facilitar nossas contas. Para isso, vamos dividir esse intervalo em 5 partes iguais e calcular a função nos extremos de cada um desses intervalos, desta forma:
![]()
Ainda não temos nenhum ponto que satisfaz , portanto vamos repetir o processo, mas agora podemos selecionar um intevalo bem melhor, que é o , pois a função nesses pontos é mais próximo de 0 que nos outros.
Vamos agora dividir o intervalo em 4 partes iguais e calcular a função nos extremos de cada um desses intervalos, desta forma:
![]()
E por ultimo, fazemos uma divisão para o intervalo
![]()
Note que satisfaz nossa condição pois
Resposta
a)Temos um ponto de descontinuidade no seguinte intervalo .
b)