Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.5 - Ex. 56
56-Suponha que seja contínua no intervalo e que para todo nesse intervalo.
a)Esboce o gráfico de junto a um gráfico possível de sobre o intervalo .
b)Use o Teorema do Valor Intermediário para ajudar a provar que existe pelo menos um número no intervalo tal que
Passo 1
a)Nosso vai ser . Ok ?
Assim,
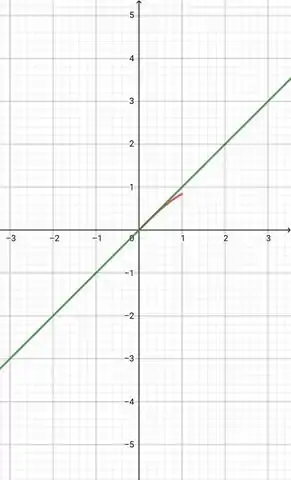
Onde o gráfico da função vermelha é e o verde de .
Passo 2
b) Galerisss, o exercício quer que a gente prove que existe pelo menos um no intervalo dado, tal que , certo ?
Podemos substituir por , né ? E, podemos fazer melhor que isso, já que . Dessa forma,
Como o enunciado diz: . Assim,
Também temos que: . Dessa forma,
Você pode estar se perguntando.... Onde que o TVI entra nessa história ????
Calma que eu já vou te mostrar....
Lembrando que o Teorema nos diz o seguinte:
Se for uma função contínua em e se e forem diferentes de zero com sinais opostos, então existe, no mínimo, uma solução para a equação no intervalo .
Caraaaa, nós que e , ou seja, e tem valores diferentes. Pelo TVI como é contínua, existe um em , tal que . Logo,
Fechou ???
Resposta
a)Gráfico acima.
b)Demonstração acima.