Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.2 - Ex. 3b
3. b) Use os testes da derivada primeira e da derivada segunda para mostrar que tem um mínimo relativo em e um máximo relativo em .
Passo 1
Então galera, de início o que vamos fazer é encontrar os pontos críticos da função que nos foi dada, ok? Derivando e igualando a zero, teremos:
Então temos dois pontos críticos, que são e , ok? Da derivada segunda temos:
Vamos guardar essa informação!
Passo 2
Beleza, agora o que temos que fazer é analisar como a função se comporta antes de , depois de , antes de e depois de , ok?
Para temos:
Ou seja, . Para temos:
Ou seja, . Por fim, para temos:
Ou seja, .
Mas o que temos que fazer com essas informações? Então galera, agora temos que analisar qual foi o comportamento da função nos intervalos! Pelo que encontramos, a função começa crescente, vira decrescente e depois crescente de novo. De crescente para decrescente isso implica um ponto de máximo, certo? Depois, de decrescente para crescente implica um ponto de mínimo, certo? Dessa forma, podemos concluir duas coisas:
é ponto de máximo;
é ponto de mínimo.
Passo 3
A fim de comprovar nosso resultado, vamos utilizar a derivada segunda que encontramos no passo 1! Para temos:
Concavidade para baixo → ponto de máximo.
Agora para temos:
Concavidade para cima → ponto de mínimo. Dessa forma, fica provado que, de fato, a função em questão tem um mínimo relativo em e um máximo relativo em . Esboçando o gráfico para garantir nosso resultado:
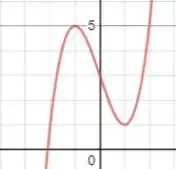
E está aí nossa prova!
Resposta
Ei, a resposta está no passo a passo :)