Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 11.1 - Ex. 1-h

1 ) Utilizando o teorema de Stokes, transforme a integral

∫ ∫ σ   ∇ × F → ⋅   n →   d S numa integral de linha e calcule.

h )   F → x , y , z = - y i → + x j → + x 2 k → ,       σ é a superfície   x 2 + y 2 + z 2 = 4 ,   2 ≤ z ≤ 3 e y ≥ 0 ,   sendo n → a normal para cima

Passo 1

Vamos calcular

∫ ∫ σ   ∇ × F → ⋅   n →   d S

Então o primeiro passo é calcular o rotacional

∇ × F → = x ^ y ^ z ^ d d x d d y d d z - y x x ²

Fazendo determinante descobrimos que

∇ × F → = 0 , - 2 x , 2

Passo 2

Agora é só questão de calcular a normal. Temos duas maneiras de calcular, você faça da maneira que se sentir mais confortável

n →   = d σ d u × d σ d v d σ d u × d σ d v

Ou

n → = ∇ σ | ∇ σ |    

Eu sempre acho mais fácil calcular pelo gradiente. No nosso caso a superfície é

x 2 + y 2 + z 2 = 4

2 ≤ z ≤ 3

y ≥ 0

OU seja é uma coroa esférica com restrições para y positivo. A imagem abaixo pode ajudar a compreender melhor

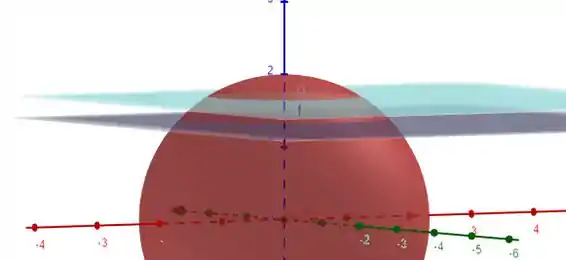
É a seção a esfera estre os planos

z = 3

z = 2

Vamos calcular essa normal.

n → = ∇ σ | ∇ σ |    

n → = 2 x , 2 y , 2 z 4 x 2 + 4 y 2 + 4 z 2 → 2 x , y , z 2 x 2 + y 2 + z 2    

Podemos usar a equação da esfera para dizer que

x 2 + y 2 + z 2 = 4

Assim a nossa normal fica

n → = x , y , z 2

Passo 3

Vamos unir o que já calculamos a nossa integração

∫ ∫ σ   ∇ × F → ⋅   n →   d S

∫ ∫ σ   0 , - 2 x , 2 ⋅   x , y , z 2 d S

1 2 ∫ ∫ σ   2 x y + 2 z   d S

∫ ∫ σ   x y + z   d S

Chegamos a um impasse temos uma função em z. Para resolver isso vamos usar a equação da esfera

x 2 + y 2 + z 2 = 4

z = 4 - x 2 - y 2

Assim nossa integração fica

∫ ∫ σ   x y + 4 - x 2 - y 2   d S

E como nossa região é circular, vamos usar as coordenadas polares para resolver

x 2 + y 2 = r 2

J = r

x = r cos ⁡ t

y = r sin ⁡ t

E como temos essas restrições

2 ≤ z ≤ 3 e y ≥ 0

Nossos intervalos de integração em Polar ficam

1 < r < 2  

0 < t < π

Assim a integral fica da seguinte maneira

∫ 1 2 ∫ 0 π cos ⁡ t sin ⁡ t + 4 - r 2 r d r d t

Podemos usar uma identidade trigonométrica

sin ⁡ 2 t = 2 cos ⁡ t sin ⁡ t

∫ 1 2 ∫ 0 π sin ⁡ 2 t 2 + 4 - r 2 r d t d r

O seno nesse intervalo será nulo, porque, se plotarmos um gráfico, a mesma área com y positivo é a mesma área com y negativo, logo elas se anulam assim podemos escrever que integrando em t obtemos

π ∫ 1 2 4 - r 2 r d r

E essa integral é fácil calcular por substituição assim obtemos

- 1 3 π 4 - r 2 3 2 1 2

=   - 1 3 π 2 3 / 2 - 3 3 / 2

= π 3 3 3 / 2 - 2 3 / 2

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

∫ ∫ σ   ∇ × F → ⋅   n →   d S = π 3 3 3 / 2 - 2 3 / 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O que é o teorema de Stokes? Como se pode interpretá-lo?
Resuma os resultados do capítulo sobre campos conservativos.
Seja S o cilindro x 2 + y 2 = a 2 , 0 ≤ z ≤ h . , juntamente com seu topo, x 2 + y 2 = a 2 , z = h . Seja F = - y i + x j + x 2 k . Utilize o teorema de Stokes para encontrar o fluxo exterior de ∇ × F
Calcule ∬ grad xx (y i) * n d sigma Onde S é o hemisfério x^2 + y^2 + z^2 = 1 , z = 0 .
Nos Exercícios 13-18, utilize a integral de superfície no teorema de Stokes para calcular o fluxo do rotacional do campo F através da superfície S na direção da normal unitária exterior n .13. F = ( y