Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 11.1 - Ex. 1-e

1 ) Utilizando o teorema de Stokes, transforme a integral

numa integral de linha e calcule.

é a superfície sendo a normal com componente x positiva

Passo 1

Vamos calcular

Entao o primeiro passo é calcular o rotacional

Fazendo determinante descobrimos que

Passo 2

Agora é só questão de calcular a normal. Temos duas maneiras de calcular, você faça da maneira que se sentir mais confortável

Ou

Eu sempre acho mais fácil calcular pelo gradiente. No nosso caso a superfície é

OU seja temos um cilindro, recortado apenas para o primeiro quadrante

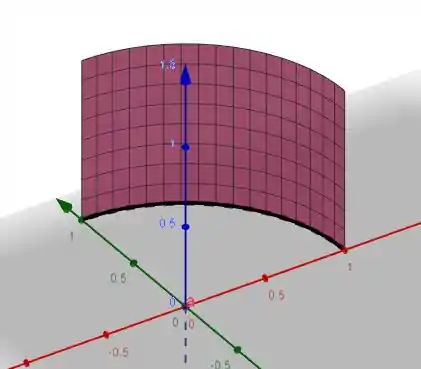
Neste formato. Vamos calcular a normal dessa superficie

Passo 3

Vamos usar o que já calculamos e unir à integral

Novamente Por causa do produto vetorial, a função para integrar será nula

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

1 ) Utilizando o teorema de Stokes, transforme a integral ∫ ∫ σ∇ × F → ⋅n →d S numa integral de linha e calcule. c )F → x , y , z = y i → + x 2 j → + z k → ,σ u , v = u , v ,2 u + v + 1 ,c o mu ≥ 0eu

1 ) Utilizando o teorema de Stokes, transforme a integral ∫ ∫ σ∇ × F → ⋅n →d S numa integral de linha e calcule. b )F → x , y , z = y i → - x 2 j → + 5 k → ,σ u , v = u , v , 1 - u 2 , c o mu ≥ 0 ,v ≥

1 ) Utilizando o teorema de Stokes, transforme a integral ∫ ∫ σ∇ × F → ⋅n →d S numa integral de linha e calcule. d )F → x , y , z = y i → + x 2 j → + z k → ,σ é a superfície x 2 + y 2 = 1 ,0z1 ,ey ≥0

1 ) Utilizando o teorema de Stokes, transforme a integral ∫ ∫ σ∇ × F → ⋅n →d S numa integral de linha e calcule. f )F → x , y , z = y i → ,σ é a superfície z =x 2 + y 2c o mz ≤ 1 sendo n → a normal co

1 ) Utilizando o teorema de Stokes, transforme a integral ∫ ∫ σ∇ × F → ⋅n →d S numa integral de linha e calcule. i )F → x , y , z = - y 2 i → + x 2 j → + z 2 k → ,σ é a superfície x 2 + y 2 4 + z 2 =