Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.5 - Ex. 27
Utilize uma calculadora gráfica com capacidade para regressão exponencial para modelar a população mundial com os dados de 1950 a 2000 da Tabela 1 da página 46. Use o modelo para estimar a população em 1993 e para predizer a população em 2010.
Passo 1
O exercício pede para fazermos um ajuste exponencial com os dados da tabela da página 46:
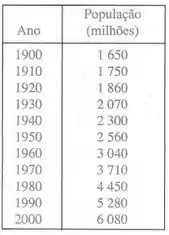
Essa tabela fornece uma população em função do tempo. A seguir plotamos os pontos:
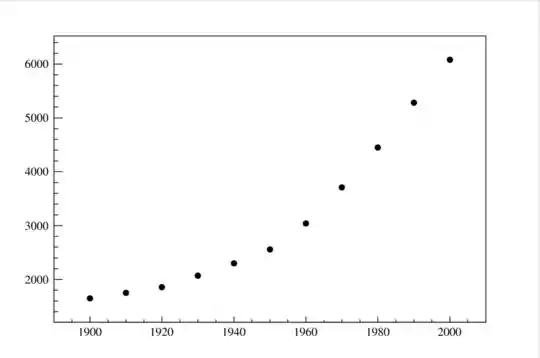
Passo 2
Para fazer o ajuste, consideramos a expressão
Usei o termo dentro da exponencial pois essa é nossa origem de tempo! Obtemos:
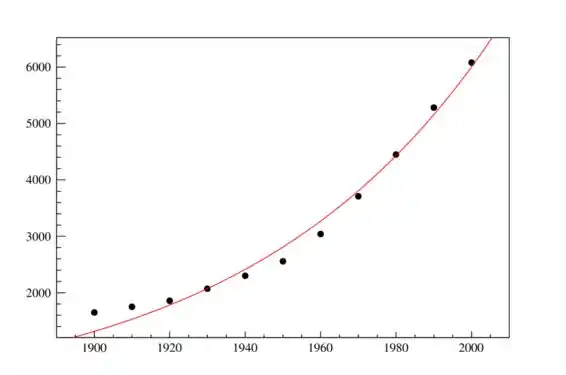
Os parâmetros do ajuste foram:
Assim,
Para :
Para :
Resposta
Ajuste gráfico.
Exercícios de Livros Relacionados
A tabela fornece a população da Malásia, em milhões, para os anos 1950-2000. Use uma calculadora gráfica com capacidade para regressão exponencial para modelar a população do país desde 1950. Utilize
Compare as funções f x = x 5 e g x = 5 x por meio de seus gráficos em várias janelas retangulares. Encontre todos os pontos de intersecção dos gráficos corretos até uma casa decimal. Para grandes valo
Encontre o domínio e esboce o gráfico da função. g ( x ) = x - 5
50. A equação Q = 12 e - 0,55 t dá a massa Q em gramas do potássio radioativo 42 que irá restar de uma quantidade inicial após t horas de decaimento redioativo.Quantas gramas havia inicialmente?Quanto
31. Suponha que o gráfico de y = 10 x tenha sido desenhado com escalas iguais de 1 cm por unidades em ambas as direções x e y. Se um besouro quiser caminhar ao longo do gráfico até alcançar uma altura