Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.8 - Ex. 16

Utilize coordenadas cilíndricas.

Determine a massa da bola B dada por x 2 + y 2 + z 2 ≤ a 2 se a densidade em qualquer ponto for proporcional à sua distância do eixo z .

Passo 1

Vamos lá pessoal. Temos um caso especial de um corpo cuja densidade varia com a distância em relação ao eixo z . Deveremos então adicionar uma constante de proporcionalidade à essa distância.Veja que a densidade é proporcional à distância do eixo z , nós podemos dizer que:

ρ x , y , z = k x 2 + y 2

Onde k é a constante de proporcionalidade.

Agora tempos que calcular a massa desse corpo da seguinte forma:

m = ∭ B ρ x , y , z d V = ∭ B k x 2 + y 2 d V

Perceba que a equação possui um termo x 2 + y 2 . Isso significa que é vantajoso utilizarmos coordendas cilíndricas de modo que x 2 + y 2 = r 2   . Veja:

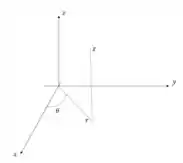
Dessa forma a coordenada r é a distância de cada ponto da origem em valor absoluto, o valor z é a distância em relação ao plano x y e o valor θ é o ângulo que r faz em relação ao eixo x .

Passo 2

Vamos identificar a região de integração, se é uma bola então sabemos que θ irá fazer uma volta completa em relação ao eixo z . De modo que:

0 < θ < 2 π

Lembre-se que a equação da esfera é da seguinte forma:

x 2 + y 2 + z 2 = a 2

Senda a o raio da esfera.

r 2 + z 2 = a 2

Então z =   a 2 - r 2  

Veja que essa integral se refere apenas aos valores positivos de z .   Porém, como a esfere é simétrica em relação ao plano x y podemos multiplicar por 2 e obter o resultado completo.

Podemos então escrever a seguinte integral:

∭ B k x 2 + y 2 d V = 2 ∫ 0 2 π ∫ 0 a ∫ 0 a 2 - r 2 k r   r d z d r d θ

Resolvendo a integral de “dentro”:

= 2 ∫ 0 2 π ∫ 0 a ∫ 0 a 2 - r 2 k r   r d z d r d θ = 2 ∫ 0 2 π ∫ 0 a ∫ 0 a 2 - r 2 k r 2 d z d r d θ

2 ∫ 0 2 π ∫ 0 a k r 2 z 0 a 2 - r 2 d r d θ

Aplicndo os intervalos:

= 2 ∫ 0 2 π ∫ 0 a k r 2 a 2 - r 2   d r d θ

Fazendo a integral em relação a r :

= 2 k ∫ 0 2 π ∫ 0 a r 2 a 2 - r 2   d r d θ

Passo 3

Para calcular essa integral vamos usar substituição trigonométrica:

r = a sen ⁡ x

d r = a cos ⁡ x d x

x = arcsen ⁡ r a

a 2 cos 2 ⁡ x = a 2 - r 2

Substituindo:

∫ a 4 cos 2 ⁡ x sen 2 ⁡ x   d x

Aplicando as fórmulas de redução de potência:

cos 2 ⁡ x = 1 + cos ⁡ 2 x 2

sin 2 ⁡ x = 1 - cos ⁡ 2 x 2

Sendo assim:

∫ 1 - cos ⁡ 2 x cos ⁡ 2 x + 1 4 d x

Fazendo as substituições da seguinte forma:

u = 2 x

x = u 2

d x = 1 2 d u

Retornando com os valores para a integral

a 4 8 ∫ 1 - cos ⁡ u cos ⁡ u + 1 2 d u

Expandindo os parênteses:

a 4 8 ∫ 1 - cos 2 ⁡ u d u

Separando em duas integrais:

a 4 8 ∫ u d u - ∫ cos 2 ⁡ u d u

a 4 8 ∙ u 0 a       -   a 4 8 ∫ cos 2 ⁡ u d u

Simplificando a integral ao lado direito:

∫ cos 2 ⁡ u d u = 1 2 ∫ cos ⁡ 2 u d u + 1 2 ∫ 1 d u

Utilizando a substituição

v = 2 u ;     u = v 2 ;     d u = 1 2 d v

1 2 ∫ cos ⁡ 2 u d u = 1 2 ∫ 1 2 cos ⁡ v   d u  

= sin �� 2 u 2

Além disso:

1 2 ∫ 1 d u = u 2

Sendo assim temos:

a 4 u 16 - a 4 sin ⁡ 2 u 32

a 4 u 8 - a 4 sin ⁡ 4 u 32

Resolvendo e retornando os valores que foram substituídos:

a 4 arcsin ⁡ r a 8 + a r 3 a 2 - r 2 4 a - a a r a 2 - r 2 8 0 a

π a 4 16 - 0

Resolvendo a integral mais de “fora”:

2 k ∫ 0 2 π π a 4 16 d θ =   π a 4 16 ∙ 2 k ∙ 2 π

Sendo assim:

m = π 2 k a 4 4

Resposta

m = π 2 k a 4 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um sólido tem a forma de um cilindro circular reto de raio de base a e altura h . Determinar o momento de inércia do sólido em relação ao eixo de simetria, se a densidade no ponto P é proporcional à d
Calcular a massa e o centro de massa do sólido delimitado por y = x 2 ,y = 9 ,z = 0ey + z = 9 , considerando a densidade de massa igual a x k g / m 3 .
Determine o centro de massa de uma semi-esfera, cuja densidade no ponto P é proporcional à distância de P ao centro.
Calcule o centro de massa da Semi-esfera homogênia x 2 + y 2 + z 2 ≤ R 2 e z ≥ 0( R0 ) .
Sabendo que a densidade em cada ponto de um sólido W é dada por f x ,y ,z = 1 x 2 + y 2 + z 2 , determine a massa de W quando W = x ,y ,z ∈ R 3|x 2 + y 2 + z 2 ≤ 9ex 2 + y 2 + z 2 ≥ 2 y