Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.8 - Ex. 8
Utilize coordenadas cilíndricas.
Calcule , onde é o sólido do primeiro octante que está abaixo do paraboloide .
Passo 1
Falaa, galera!
Nessa questão a gente precisa calcular uma integral tripla sobre um sólido , usando coordenadas cilíndricas.
Precisamos lembrar das relações entre as coordenadas cartesianas e cilíndricas :
O que vamos fazer é descrever o sólido em termos de coordenadas cilíndricas, pra transformar nossa integral em integral iterada e calcular!
Passo 2
Primeira coisa que vamos fazer é olhar por sólido, que está abaixo do paraboloide:
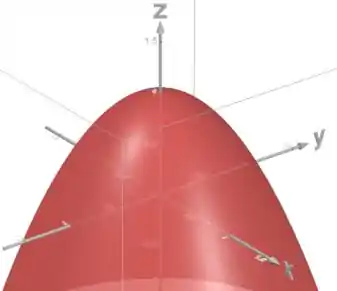
Só que estamos só no primeiro octante (). Então o sólido fica assim:
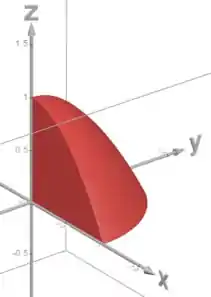
A coordenada está entre o plano () e o paraboloide, então:
Já as outras duas coordenadas ( e , que vão virar e ), vamos ver pela projeção do sólido no plano .
O limite dessa região vai ser a circunferência que é a interseção do paraboloide com o plano :
Igualando o das duas equações:
O que é uma circunferência centrada na origem de raio :
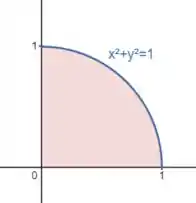
E ai a gente já entende porque usamos coordenadas cilíndricas! Temos uma região circular no plano – vamos transformar esse em .
Estamos dentro de um círculo de raio , então
E estamos no primeiro quadrante, então
Voltando pros limites de :
Como estamos em coordenadas cilíndricas,
E temos todos os nossos limites:
Passo 3
Duas informações importantes que temos que usar antes de transformar a integral em integral iterada:
- Como os limites de dependem de , teremos que integrar antes de
- Fizemos uma mudança de variáveis, então temos que multiplicar o jacobiano dentro do integrando, que no caso de coordenadas cilíndricas é .
Então vamos pra nossa integral:
A gente precisa transformar esse integrando em coordenadas cilíndricas:
Agora mudando as variáveis (lembrando que ):
Voltando pra integral, fica assim:
Beleza... agora vamos partir pras contas!
Temos que integrar isso de dentro pra fora:
Passo 4
Primeiro integrando em função de , mantendo e constantes:
Como o integrando não depende de , podemos tirar da integral, e calcular:
Substituindo nos limites de integração:
Passo 5
Agora integramos em função de , mantendo como constante:
Como é constante em função de , podemos tirar dessa integral:
Calculando nos limites:
Passo 6
Por último, integramos em função de :
Substituindo nos limites:
Então, temos o resultado da integral: