Utilize uma ferramenta gráfica para desenhar um silo que consista em um cilindro de raio e altura com um hemisfério no topo.
Passo 1
Oi galera, tudo bem?
Essa questão pede pra gente usar uma ferramenta gráfica pra desenhar um silo...
Primeiro de tudo: você sabe o que é um silo?? 👀
É isso aqui ó:

Bom, a questão falou que o nosso silo vai ser composto de um cilindro de raio e altura , e com um hemisfério no topo. Então, diferente desse aí da foto, o “teto” do nosso silo vai ser metade de uma esfera (que é um hemisfério).
Vamos definir quais equações que descrevem esse silo que a gente quer e jogar isso num software (o que eu vou usar é o Desmos) pra ele desenhar!
Passo 2
Primeiro, vamos ver o cilindro.
Ele é um cilindro de raio , vamos fazer na direção de , então é a mesma equação de uma circunferência no plano :
Como nós queremos uma altura de , vamos limitar o :
Vamos colocar isso no Desmos pra ver como fica o cilindro:
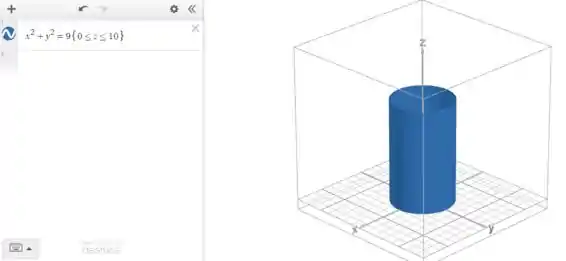
Percebe que colocamos entre chaves a limitação das variáveis (nesse caso, só tinha em ).
Passo 3
Para a “tampa” do silo, queremos plotar metade de uma esfera.
Só que percebe que pra essa esfera ficar exatamente em cima do cilindro que a gente desenhou, o centro dela tem que estar a uma altura , e bem em cima do eixo . Ou seja:
Além disso, pras duas superfícies se encaixarem, elas têm que ter o mesmo raio .
Então a equação dessa esfera é:
Se a gente jogar só essa equação lá, o Desmos vai plotar a esfera inteira. Pra pegarmos só o hemisfério de cima, temos que limitar a esfera a parte a cima da altura do centro, ou seja:
Então:
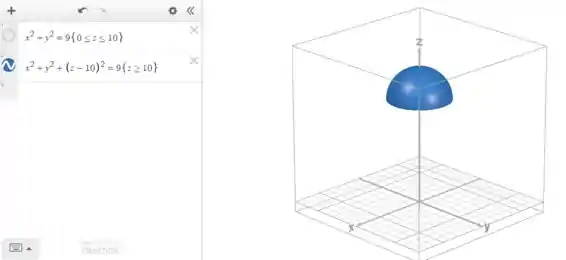
Passo 4
Plotando as duas superfícies juntas, temos o nosso silo:

Resposta