Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.7 - Ex. 18

Utilize coordenadas cilíndricas

Calcule ∭ E z d V , onde E é limitado pelo paraboloide z = x 2 + y 2 e o plano z = 4 .

Passo 1

Faala, pessoal!

Essa questão pede pra calcularmos uma integral usando coordenadas cilíndricas!

Primeiro vamos perceber que essa região de integração é uma região do tipo I, ou seja, z está entre duas funções de x , y , e x , y pertencem a um domínio D no plano x y . Nesse tipo de região temos:

∭ E z d V = ∬ D ∫ g 1 x , y g 2 x , y z d z d A

Esse domínio D vai ser um equivalente a coordenadas polares, e nossa mudança para coordenadas cilíndricas fica assim:

x = r cos ⁡ θ y = r sen ⁡ θ z = z

O que vamos fazer é usar as superfícies que limitam o sólido E pra definir quem são g 1 e g 2 , e qual é o domínio D .

Assim, transformamos nossa integral em uma integral iterada, e calculamos normalmente, de dentro pra fora.

Passo 2

Nosso sólido está entre z = 4 e o paraboloide z = x 2 + y 2 . Vamos esboçar isso:

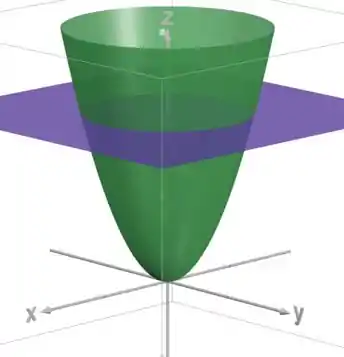
Percebe que a região entre as duas superfícies está abaixo do plano e acima do paraboloide, então:

x 2 + y 2 ≤ z ≤ 4

Então:

∭ E z d V = ∬ D ∫ x 2 + y 2 4 z d z d A

Agora vamos olhar para a projeção disso no plano x y :

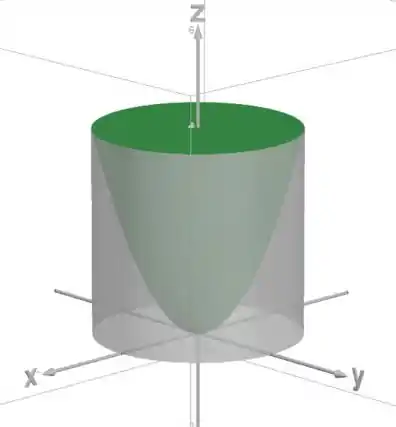
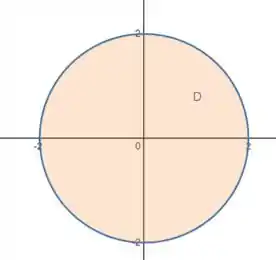
Isso fica um disco de raio 2 :

Em coordenadas cilíndricas, usamos:

x = r cos ⁡ θ y = r sen ⁡ θ z = z

E como temos o disco inteiro,

0 ≤ r ≤ 2

0 ≤ θ ≤ 2 π

E isso define o D .

Voltando para os limites de z :

x 2 + y 2 ≤ z ≤ 4

Em coordenadas cilíndricas x 2 + y 2 = r 2 , então:

r 2 ≤ z ≤ 4

Então nossa integral fica:

∭ E z d V = ∬ D ∫ r 2 4 z d z d A

Agora vamos substituir os limites de D , sem esquecer de multiplicar o jacobiano J = r :

∭ E z d V = ∫ 0 2 ∫ 0 2 π ∫ r 2 4 z ∙ r d z d θ d r

Passo 3

Começamos integrando em função de z , considerando r e θ constante:

= ∫ 0 2 ∫ 0 2 π ∫ r 2 4 z r d z d θ d r =

= ∫ 0 2 ∫ 0 2 π r ∙ z 2 2 z = r 2 z = 4 d θ d r =

Substituindo os limites de integração:

= ∫ 0 2 ∫ 0 2 π r ∙ 4 2 2 - r 2 2 2 d θ d r =

= ∫ 0 2 ∫ 0 2 π r ∙ 8 - r 4 2 d θ d r =

Agora integrando em função de θ , com r constante:

= ∫ 0 2 ∫ 0 2 π r ∙ 8 - r 4 2 d θ d r =

= ∫ 0 2 r ∙ 8 - r 4 2 ∙ θ 0 2 π d r =

Então:

= ∫ 0 2 r ∙ 8 - r 4 2 ∙ 2 π - 0 d r =

= ∫ 0 2 2 π r ∙ 8 - r 4 2 d r =

Vamos tirar o 2 π da integral e fazer a distributiva desse r :

= 2 π ∫ 0 2 8 r - r 5 2 d r =

Por último, integrando em função de r :

= 2 π 8 r 2 2 - r 6 12 0 2 =

= 2 π 8 ∙ 2 2 2 - 2 6 12 - 0 =

Então:

= 2 π 16 - 64 12 = 2 π 16 - 16 3 =

= 2 π ∙ 32 3

E achamos o valor da integral:

∭ E z d V = 64 π 3

Resposta

∭ E z d V = 64 π 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cilindro e paraboloide Encontre o volume da região delimitada inferiormente pelo plano z = 0, lateralmente pelo cilindrox2 + y2 = 1 e superiormente pelo paraboloide z = x2 + y2.
Encontre os volumes dos sólidos nos Exercícios 43-48.
Paraboloide e cilindro Encontre o volume da região delimitada superiormente pelo paraboloide z = 9 – x2 – y2, inferiormente pelo plano xy e fora do cilindro x2 + y2 = 1.
Cilindro e paraboloides Encontre o volume da região delimitada inferiormente pelo paraboloide z = x2 + y2, lateralmente pelo cilindro x2 + y2 = 1 e superiormente pelo paraboloidez = x2 + y2 + 1.
Região delimitada por paraboloides Encontre o volume daregião delimitada superiormente pelo paraboloide z = 5 – x2 – y2e inferiormente pelo paraboloide z = 4x2 + 4y2.