Enunciado
Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 14.7 - Ex. 28
Utilize uma ferramenta gráfica como no Exemplo 4 (ou o Método de Newton ou um determinador de raízes) para encontrar os pontos críticos de com precisão de três casas decimais. Em seguida, classifique o ponto crítico e determine o valor mais alto e o mais baixo do gráfico.
Passo 1
A função que ele nos deu foi a seguinte:
e queremos determinar os seus pontos críticos com o auxílio de uma ferramenta gráfica. Depois disso, classificaremos esses pontos entre máximo, mínimo e ponto de sela.
Como ele nos dá a opção de utilizar uma ferramenta gráfica, vamos fazer isso! Esboçando um gráfico para , temos:
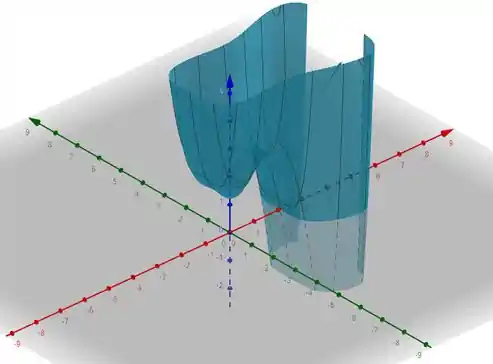
A partir de agora usaremos esse gráfico para nos auxiliar nas próximas análises.
Passo 2
Para o ponto de mínimo, temos:
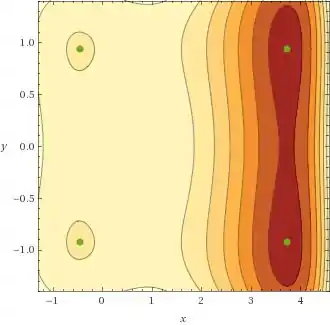
Os pontos de críticos os pontos verdes marcados no gráfico acima são o seguinte:
; ; e
Agora vamos calcular os valores de para esses pontos:
Analisando o primeiro gráfico e os pontos críticos, concluímos que os pontos de mínimos são:
e
Passo 3
Para os pontos de máximo:
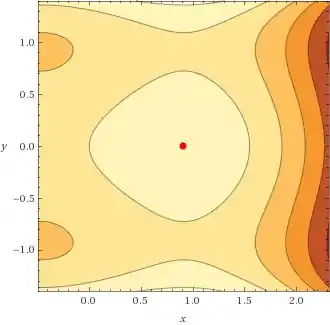
Esse ponto vermelho é o seguinte:
Logo,
Portanto, o ponto de máximo será
Resposta
Os pontos de mínimos são:
e
o ponto de máximo será