Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.Exercícios práticos - Ex. 81b

Utilize um gráfico para decidir se é uma função injetora.

Passo 1

Fala, galera! Olha só, ele quer apenas que você monte um gráfico, olhe pra ele e diga se é injetora ou não. Mas o que é uma função injetora? É aquela que, se você tem e diferentes, a imagem deles, ou seja, e , vai ser diferente. Pra facilitar ainda mais, saiba que é só você olhar pro gráfico e traçar linhas horizontais. Se essas linhas cruzarem o gráfico mais de uma vez, a função NÃO É injetora. Mas, se cruzarem apenas uma vez, ela É injetora. Vamos lá?

Passo 2

O gráfico da nossa função é esse:

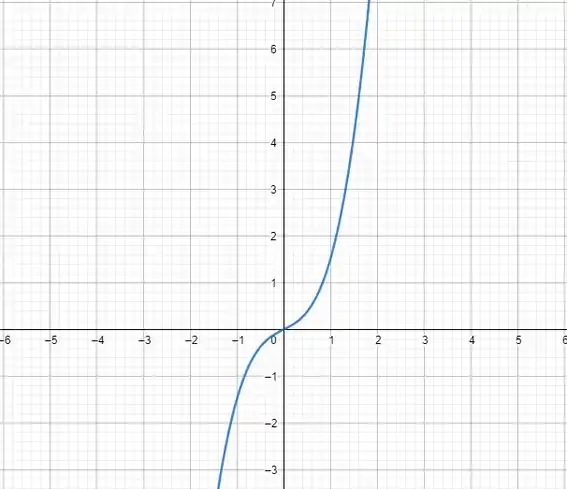
Se você pegar qualquer reta horizontal, vai ver que ela cruza o gráfico apenas uma vez. Você pode pegar uma régua ou um lápis aí na sua casa, colocar paralelo ao eixo x pra ver quantas vezes o gráfico encosta no lápis ou na régua e verificar que é injetora.

Resposta

Ela é injetora.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre uma equação da forma y = y 0 + A s e n B x - C para cada gráfico.

Nos EUA, as tomadas elétricas padrão fornecem uma corrente elétrica senoidal com uma voltagem máxima de V = 120 2 volts (V), a uma frequência de 60 hertz (Hz). Escreva uma equação que expresse Vcomo u

Encontre a amplitude e o período e esboce pelo menos dois períodos do gráfico à mão. Confira seu trabalho com um recurso gráfico.(a) y = 3 s e n ( 4 x ) (b) y = - 2 c o s ⁡ ( π x ) (c) y = 2 + cos ⁡ x

Encontre a amplitude e o período e esboce pelo menos dois períodos do gráfico à mão. Confira seu trabalho com um recurso gráfico.(a) y = - 1 - 4 s e n ( 2 x ) (b) y = 1 2 c o s ⁡ ( 3 x - π ) (c) y = -

Expresse a equação: x = 5 3 s e n 2 π t + 5 2 c o s ⁡ ( 2 π t ) Na forma x = A s e n ( ω t + θ ) e use um recurso gráfico para confirmar que ambas as equações têm o mesmo gráfico.