Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.4 - Ex. 11

Calcule a integral dada, colocando-a em coordenadas polares.

∬ D   e - x 2 - y 2   d A ,

onde D é a região delimitada pelo semicírculo x = 4 - y 2 e o eixo y .

Passo 1

Olá, pessoal! tudo bem? Vamos entender o que a questão está pedindo.

Ela quer que a gente calcule a integral dupla

∬ D   e - x 2 - y 2   d A ,

mudando x , y para coordenadas polares.

Que da definição de coordenadas polares, temos que

x = r cos ⁡ θ

y = r sen ⁡ θ

Onde D é delimitado pelo semicírculo

x = 4 - y 2

E o eixo y .

Portanto, vamos primeiro encontrar a região D , depois iremos achar os limites de integração, depois fazer a substituição de coordenadas e finalmente calcular a integral.

Show?

Passo 2

Então, galerinha, primeiro de tudo, vamos esboçar essa tal região D e ver se ela é isso tudo mesmo. O enunciado disse pra gente que

x = 4 - y 2

Reorganizando os termos, eu tenho que

x 2 = 4 - y ²

x 2 + y 2 = 4

Temos aqui a equação de uma circunferência de raio 2

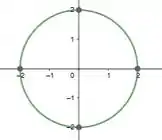
MAAASSS como nem tudo é um mar de rosas, quando o enunciado diz x = 4 - y 2 , ele na verdade quer dizer x = + 4 - y 2 , ou seja, queremos somente a parte positiva do eixo x, então a região D na verdade é

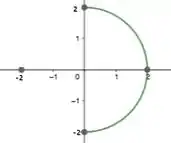
Passo 3

Agora que a gente já sabe a região, podemos definir as substituições e os intervalos. Temos então que

x = r cos ⁡ θ

y = r sin ⁡ θ

O nosso ângulo vai estar variando de acordo com a região D, dado o círculo trigonométrico e a região que vimos é

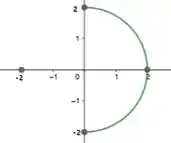
Ou seja,

- π 2 < θ < π 2

Já o r vai variar de zero até seu valor máximo

0 < r < 2

Passo 4

Agora sim podemos escrever nossa integral em coordenadas polares

Temos então que

∬ D   e - x 2 - y 2   d A = ∬ D   e - ( x 2 + y 2 )   d A

E sendo

x = r cos ⁡ θ

y = r sin ⁡ θ

Elevamos x e y ao quadrado e depois somamos:

x 2 + y 2 = r 2 cos 2 ⁡ θ + r 2 sin 2 ⁡ θ

x 2 + y 2 = r 2 cos 2 ⁡ θ + sin 2 ⁡ θ

Lembra que cos 2 ⁡ θ + s e n 2 θ = 1 .

x 2 + y 2 = r 2

Então:

∬ D   e - ( x 2 + y 2 )   d A =   ∬ D     e - r ²     d A

Lembrando que quando a substituição é para coordenadas polares, d A = r   d r   d θ .

∬ D     e - r ²     d A = ∬ D     r e - r ²     d r d θ

Colocando os limites

0 < r < 2

- π 2 < θ < π 2

A nossa integral fica:

∬ D     r e - r ²     d r d θ = ∫ - π / 2 π / 2 ∫ 0 2 r   e - r ²   d r d θ

Passo 5

Vamos resolver essa integral

∫ - π / 2 π / 2 ∫ 0 2 r   e - r ²   d r d θ

por substituição simples. Fazendo

u = - r 2

Temos que derivando u em relação à r

d u = - 2 r   d r

d u = - 2 r   d r

d u - 2 r = d r

Achando os novos limites de integração, temos que quando   r = 2

u = - r 2

u = - 4

Mas precisamos apenas do valor positivo

u = 4

Quando r = 0

u = - r 2

u = 0

Logo,

∫ - π / 2 π / 2 ∫ 0 2 r   e - r ²   d r d θ = ∫ - π / 2 π / 2 ∫ 0 4 -   e u   2 r r d u d θ

∫ - π / 2 π / 2 ∫ 0 4 -   e u   2 r r d u d θ = ∫ - π / 2 π / 2 ∫ 0 4 -   e u   2 d u d θ

Resolvendo para d u :

∫ - π / 2 π / 2 ∫ 0 4 -   e u   2 d u d θ = ∫ - π / 2 π / 2 -   e u   2 0 4 d θ

substituindo os limites:

∫ - π / 2 π / 2 -   e u   2 0 4 d θ = ∫ - π / 2 π / 2 - e - 4 2 - - e 0 2 d θ

Simplificando as expressões:

∫ - π / 2 π / 2 - e - 4 2 - - e 0 2 d θ = ∫ - π / 2 π / 2 1 2 - e - 4 2 d θ

Colocando 1 2 em evidência:

∫ - π / 2 π / 2 1 2 - e - 4 2 d θ = ∫ - π / 2 π / 2 1 2 1 - e - 4 d θ

Resolvendo para d θ :

∫ - π / 2 π / 2 1 2 1 - e - 4 d θ = 1 2 1 - e - 4 θ - π / 2 π / 2

Aplicando os limites:

1 2 1 - e - 4 θ - π 2 π 2 = 1 2 1 - e - 4 π 2 - - π 2

Colocando o 1 2 dos parênteses em evidência

1 2 1 - e - 4 π 2 - - π 2 = 1 4 1 - e - 4 π + π

Somando os π ’s

1 4 1 - e - 4 π + π = 1 4 1 - e - 4 2 π

Simplificando

1 4 1 - e - 4 2 π = π 2 1 - e - 4

Ala ela, a cara do coisa ruim, isso quer dizer que

∬ D   e - x 2 - y 2   d A = π 2 1 - e - 4

Resposta

π 2 ( 1 - e - 4 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 9-22, substitua a integral cartesiana por uma integral equivalente. Em seguida, calcule a integral polar. ∫ - 1 1 ∫ - 1 - x 2 1 - x 2 2 1 + x 2 + y 2 d yd x
Nos Exercícios 9-22, substitua a integral cartesiana por uma integral equivalente. Em seguida, calcule a integral polar. ∫ 0 1 ∫ x 2 - x 2 x + 2 y d yd x
Nos Exercícios 23-26, esboce a região de integração e converta cada uma das integrais polares ou soma de integrais a uma integral cartesiana ou soma de integrais. Não calcule as integrais. ∫ 0 π 2 ∫ 0
Fórmula da área em coordenadas polares: Utilize a integral dupla em coordenadas polares para deduzir a fórmula: A = ∫ α β 1 2 r 2 d θ para a área da região em formato de leque entre a origem e a curva
Suponha que a área de uma região no plano de coordenadas polares seja A = ∫ π 4 3 4 π ∫ c o s s e c θ 2s e n θ rd rd θ Esboce a região e encontre sua área.