Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.3 - Ex. 32
Ache o centroide da região limitada pelas curvas.
Passo 1
Beleza galera, Yuri aqui e estarei ajudando a resolver essa atividade.
Nessa questão queremos encontrar o centroide delimitado pelas curvas. Para isso, iremos calcular as coordenadas exatas do centroide utilizando as definições do centroide utilizando integrais.
Baixo está o gráfico da região que iremos trabalhar:
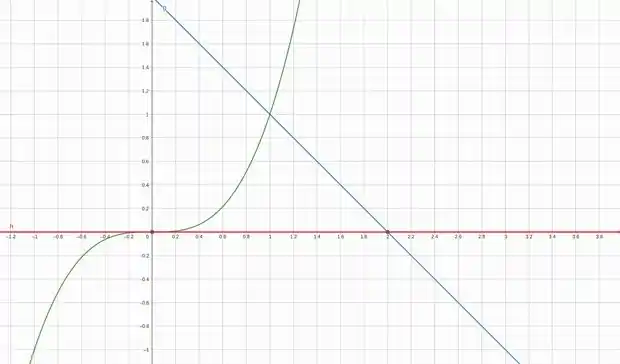
Sendo a curva vermelha, a curva azul e a curva verde.
Por definição, temos que
Onde são as coordenadas dos centroides, A é a área da região, e e o intervalo da região para qual estamos querendo encontrar o centroide.
Passo 2
Dessa forma, temos que
Veja que estamos dividindo a nossa integral em duas, estamos calculando primeiramente a área da região do gráfico da função até o encontro dela com a função , que acontece em , depois calculamos a área da região do gráfico de . Podemos ver abaixo a divisão que iremos fazer em relação as duas regiões distintas que iremos trabalhar.
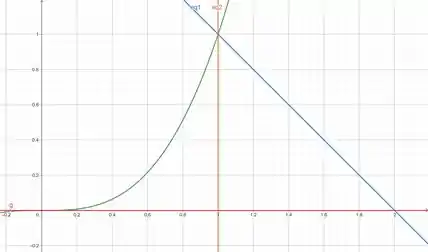
Passo 3
Calculando utilizando as definições do passo anterior, temos
Aqui também utilizamos o mesmo princípio da divisão das regiões como no passo anterior.