Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.2 - Ex. 51
Utilize vetores para demonstrar que uma reta unindo os pontos médios de dois lados de um triângulo é paralela ao terceiro lado e tem metade de seu comprimento.
Passo 1
Bom, vamos desenhar um triângulo arbitrário, com vértices em e , então ele será formado pelos vetores e , assim:
Agora vamos marcar o ponto médio de , e o ponto médio de . Aí podemos desenhar os vetores e
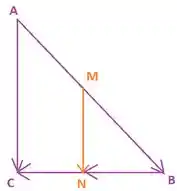
Basta mostrarmos que . Então teremos provado que o segmento que une os pontos médios de dois lados de um triângulo é paralelo ao terceiro lado, e tem metade do seu comprimento.
Assim, concluímos que uma reta unindo os pontos médios de dois lados de um triângulo é paralela ao terceiro lado e tem metade de seu comprimento.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
O vetor v → é ortogonal aos vetores u → = 1,2 , 0 e w → = 2,0 , 1 e forma ângulo agudo com o vetor j → . Determinar v → , sabendo que v → = 21 .
Determinar o vetor a → de módulo 5 , sabendo que é ortogonal ao eixo O y e ao vetor v → = i → - 2 k → , e forma ângulo obtuso com o vetor i → .
Seja o cubo de aresta a representado na Figura 2.17 . Determinar:o ângulo agudo formado por duas diagonais do cubo.
Seja o cubo de aresta a representado na Figura 2.17 . Determinar:o ângulo agudo entre a diagonal do cubo e uma aresta.
Os ângulos diretores de um vetor a → são 45 ° , 60 ° e 120 ° e a → = 2 . Determinar a → .