Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 2.Problemas Propostos - Ex. 31g
Seja o cubo de aresta representado na Figura . Determinar:
o ângulo agudo entre a diagonal do cubo e uma aresta.
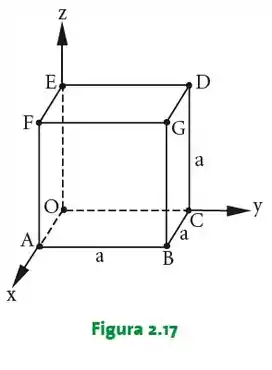
Passo 1
Primeiro vamos ver na figura o ângulo agudo entre a diagonal do cubo e uma aresta:
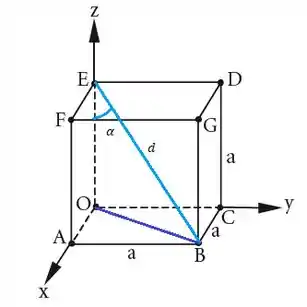
Vamos achar o valor da diagonal da figura:
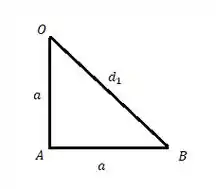
Passo 2
Agora temos o outro triangulo, com a diagonal e a aresta pedida no enunciado:
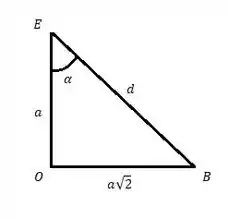
Temos então que o ângulo pode ser achado pela tangente de tirada da figura acima, vamos lá então:
Resposta
Exercícios de Livros Relacionados
Encontre as derivadas das funções vetoriais. r t = t - 2 , 3 , 1 t 2
Esboce o gráfico da curva plana com a equação vetorial dada.Encontre r ' ( t ) .Esboce o vetor posição r ( t ) e o vetor tangente r ' ( t ) para o valor dado de t . r t = e 2 t i ^ + e t j ^
Esboce o gráfico da curva plana com a equação vetorial dada.Encontre r ' ( t ) .Esboce o vetor posição r ( t ) e o vetor tangente r ' ( t ) para o valor dado de t . r t = cos t + 1 i ^ + sen t - 1
Esboce o gráfico da curva plana com a equação vetorial dada.Encontre r ' ( t ) .Esboce o vetor posição r ( t ) e o vetor tangente r ' ( t ) para o valor dado de t . r t = 4 s e nt i ^ - 2 cos t j ^
Esboce o gráfico da curva plana com a equação vetorial dada.Encontre r ' ( t ) .Esboce o vetor posição r ( t ) e o vetor tangente r ' ( t ) para o valor dado de t . r t = 4 s e nt i ^ - 2 cos t j ^