Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 2.Problemas Propostos - Ex. 31h

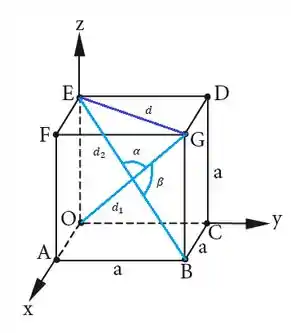
Seja o cubo de aresta a representado na Figura 2.17 . Determinar:

o ângulo agudo formado por duas diagonais do cubo.

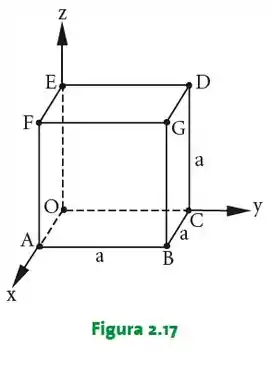
Passo 1

Primeiro vamos ver na figura o ângulo agudo α entre as duas diagonais do cubo d 1 e d 2 :

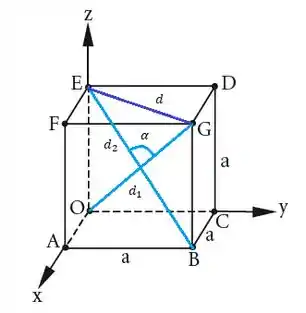
Agora vamos usar a definição geométrica do produto escalar para encontrar o ângulo α , nós temos que se u → e v → são vetores não nulos e θ o ângulo entre eles temos:

u → ⋅ v → = u → v → cos ⁡ θ

Vamos aplicar a nossa questão, sendo u → = O G → e v → = B E → :

O G →   ⋅ B E → = O G → B E → cos ⁡ α

Passo 2

Primeiro vamos encontrar os dois vetores:

O G → = G - O

B E → = E - B

Temos então que achar os pontos G , O , E e B de acordo com a figura:

G = a , a , a

O = 0,0 , 0

E = 0,0 , a

B = a , a , 0

Passo 3

Agora sim vamos então encontrar os vetores:

O G → = G - O = a , a , a - 0,0 , 0 = a - 0 , a - 0 , a - 0 = a , a , a

B E → = E - B = 0,0 , a - a , a , 0 = 0 - a , 0 - a , a - 0 = - a , - a , a

Falta agora encontrar os módulos, vamos lá:

O G → = a 2 + a 2 + a 2 = 3 a 2 = a 3

B E → = - a 2 + - a 2 + a 2 = 3 a 2 = a 3

E por último vamos fazer o produto escalar, lembrando que ele é feito desse jeito: chama-se produto escalar de dois vetores u → = x 1 , y 1 , z 1 e v → = x 2 , y 2 , z 2 , representado por u → ⋅ v → , o número real encontrado pela seguinte soma:

u → ⋅ v → = x 1 x 2 + y 1 y 2 + z 1 z 2

Vamos aplicar agora na nossa questão:

O G →   ⋅ B E → = a , a , a   ⋅ - a , - a , a = a - a + a - a + a ⋅ a = - a 2 - a 2 + a 2 = - a 2

Passo 4

Pronto, agora é só aplicar na fórmula:

O G →   ⋅ B E → = O G → B E → cos ⁡ α → - a 2 = a 3 ⋅ a 3 cos ⁡ α → - a 2 = 3 a 2 cos ⁡ α →

→ - 1 = 3 cos ⁡ α → α = arccos ⁡ - 1 3 = 109 ° 28 '

Eita, achamos não o ângulo agudo, pois um ângulo agudo está entre 0 ° e 90 ° , temos então que para achar o ângulo agudo é só subtrair de 180 ° o ângulo que achamos:

β = 180 ° - α = 180 ° - 109 ° 28 ' = 70 ° 31 '

Vamos ver ele na figura:

Resposta

β = 70 ° 31 '

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o ponto na curva de r t = 2 cos ⁡ t ,2s e nt ,e t , 0 ≤ t ≤ π , em que a reta tangente é paralela ao plano 3 x + y = 1 .
Encontre uma equação para a reta tangente à curva de intersecção dos cilindros x 2 + y 2 = 25 e y 2 + z 2 = 20 no ponto 3 ,4 ,2 .
Determine o vetor tangente unitário T ( t ) no ponto com valor de parâmetro dado t . r → t = tan - 1 ⁡ t , 2 e 2 t , 8 t e t ,t = 0
Determine a derivada da função vetorial. r t = s e n 2a t i + t e b t j + cos 2 ⁡ c t k
Encontre as derivadas das funções vetoriais. r t = e - t ,t - t 3 , ln ⁡ t