Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.5 - Ex. 57
Mostre que as retas tangentes à parábola desenhadas a partir de um ponto qualquer na diretriz são perpendiculares.
Passo 1
Olá, meu amigo. Vou te ajudar aqui nessa atividade. Fique tranquilo que daqui você já vai sair sabendo resolver essas e outras questões do tipo fácil fácil.
Queremos mostrar que as retas tangentes à parábola desenhadas em um ponto qualquer da diretriz são perpendiculares.
Para ficar mais fácil de entender isso, podemos olhar o desenho:
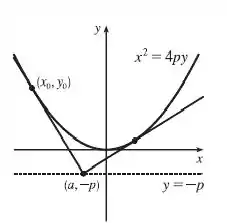
Deveremos então encontrarmos as nossas retas tangentes.
Então a reta tangente em um ponto é
A primeira coisa que precisamos é da inclinação da reta tangente, que é dada derivando a função
Bom, vamos derivar nossa equação para encontrar a inclinação:
Lembre-se de que: o produto da inclinação de duas retas perpendiculares é . Então teremos duas retas tangentes com inclinações e e o produto entre elas deverá ser:
Passo 2
De tiramos que , aí podemos trocar isso na equação da reta tangente:
Essa reta passa pelo ponto da diretriz, então substituindo esse ponto:
Multiplicando tudo por :
Essa é hora que nós vamos dar o pulo do gato: completar quadrado!
A inclinação das linhas tangentes em .
Como :
Passo 3
Fazendo o produto dessas duas inclinações, ficamos com
Mas o que isso quer dizer? Bom, agora precisamos lembrar das aulas de geometria analítica, quando aprendemos que sempre que a multiplicação da inclinação de duas retas for igual a nós temos duas retas perpendiculares.
Assim, provamos o que queríamos.
Resposta
Demonstração.