Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.4 - Ex. 14
Para um valor fixo de (digamos ), a família de funções logísticas dada pela Equação depende do valor inicial e da constante de proporcionalidade . Trace vários membros dessa família. Como muda o gráfico quando varia? Como muda o gráfico quando varia?
Passo 1
Beleza, galera? Primeiro, vamos ver como é essa família de funções logísticas de quem o enunciado fala:
Vamos fazer de forma que nossa família de funções vai ser da seguinte forma:
Passo 2
Agora, bora ver como o gráfico muda quando varia? Pra isso, vamos deixar o valor de fixo, beleza?
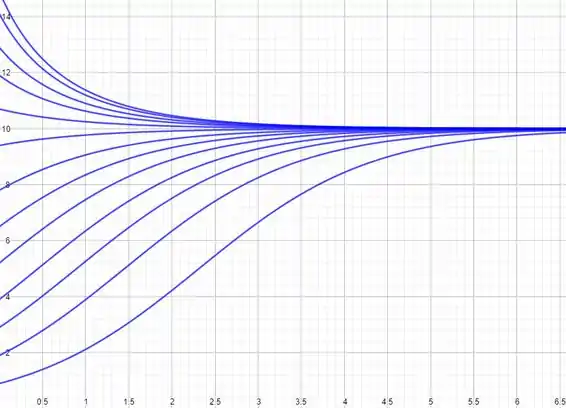
À medida que aumenta, os gráficos começam em pontos cada vez mais altos, pois . Repare que se , os gráficos são crescentes, e se são decrescentes.
No final das contas, todas as soluções acabam crescendo ou decrescendo para , né mesmo?
Passo 3
Agora vamos deixar o valor de fixo, pra gente ver como o gráfico muda quando varia, pode ser?
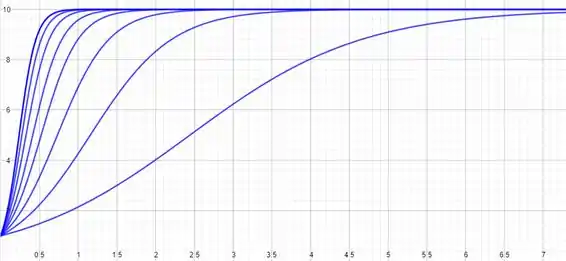
Lembre-se que quanto maior o valor de , maior é a taxa de crescimento inicial relativo , então maior é a inclinação da curva no início. Repare que maiores valores de , portanto, fazem com que a curva tenda mais rápido à solução de equilíbrio .
Veja que a curva mais “baixa”, a que começa com menor inclinação (mais horizontal), feita a partir do menor valor de , é a que mais demora pra se aproximar de !
Resposta
Ei, a resposta está no passo a passo :)