Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.7 - Ex. 20

Para que valor(es) de x obteremos c o s (x) = - x ?

Passo 1

Para obtermos cos (x) = - x separaremos em duas funções e vamos plotar o gráfico para ver o ponto de intersecção entre eles. Dessa forma, tomemos y 1 = - x e y 2 = cos (x) , plotando o gráfico vamos obter

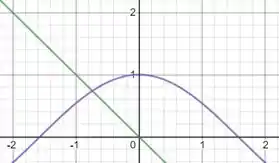
Podemos reparar que existe um valor que se encontra entre -1 e 0 e é exatamente eles quem queremos estimar utilizando o método de Newton que nos diz que

x_n + 1 = x_n - (f ( x_n ))/(f ' ( x_n ))

Passo 2

Primeiramente vamos derivar a função, para poder substituir na fórmula do método de Newton. Assim,

f (x) = cos (x) + x -> f^' (x) = 1 - s e n (x)

Tomando, também, um valor intermediário no intervalo como valor inicial poderemos estimar nossa raiz, assim pegando x 0 = - 0 . 7 podemos substituir na fórmula obtendo

x_n + 1 = x_n - (cos (x_n) + x_n)/(1 - s e n (x_n))

Na nossa primeira iteração, vamos obter

x_0 + 1 = x_0 - (cos (x_0) + x_0)/(1 - s e n (x_0))

x_1 = - 0.7 - (cos (- 0.7) - 0.7)/(1 - s e n (- 0.7))

x_1 tildetilde - 0 . 73944

Para nossa próxima iteração utilizaremos o valor de x_1 como valor inicial e faremos

x_1 + 1 = x_1 - (cos (x_1) + x_1)/(1 - s e n (x_1))

x_2 = - 0.73944 - (cos (- 0.73944) - 0.73944)/(1 - s e n (- 0.73944))

x_2 tildetilde - 0.73908

Portanto, podemos pegar - 0 . 74 como uma boa aproximação para termos cos (x) = - x

Resposta

Para x tildetilde - 0 . 74 temos cos (x) = - x

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 15 a 18, use o método de Newton para encontrar, com quatro casa decimais, a coordenada x do ponto de interseção no primeiro quadrante dos gráficos das duas equações.
Equações da forma t gx + a x = 0 , onde a é inteiro, surgem em problemas de condução de calor. As raízes positivas da equação em ordem crescente são a 1 ,a 2 ,a 3 , … Se a = 1 , ache a 1ea 2 com quatr
Nos exercícios de 15 a 18, use o método de Newton para encontrar, com quatro casa decimais, a coordenada x do ponto de interseção no primeiro quadrante dos gráficos das duas equações.
Nos exercícios de 15 a 18, use o método de Newton para encontrar, com quatro casa decimais, a coordenada x do ponto de interseção no primeiro quadrante dos gráficos das duas equações.
Nos exercícios de 15 a 18, use o método de Newton para encontrar, com quatro casa decimais, a coordenada x do ponto de interseção no primeiro quadrante dos gráficos das duas equações.