Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.1 - Ex. 38 (a)
Variação dos Parâmetros. Considere o seguinte método de resolução da equação linear de
primeira ordem geral:
(i)
- Se g(t) = 0 para todo t, mostre que a solução é
- Se g(t) não é identicamente nula, suponha que a solução da Eq. (i) é da forma
- Encontre A(t) da Eq. (iv). Depois substitua A(t) na Eq. (iii) e determine y. Verifique se a
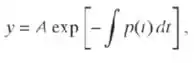(ii)
em que A é uma constante.
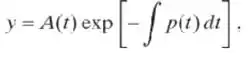(iii)
em que A agora é uma função de t. Substituindo y na equação diferencial dada, mostre que A(t) tem que satisfazer a condição
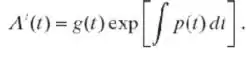(iv)
solução obtida dessa maneira é igual à solução da Eq. (33) no texto. Essa técnica é conhecida
como o método de variação dos parâmetros; é discutida em detalhes na Seção 3.6 em conexão com equações lineares de segunda ordem.
Passo 1
- Ao observarmos a equação (i) percebemos que trata-se de uma EDO de primeira ordem, pois temos a primeira derivada da função y. Dessa forma, para acharmos a solução para essa equação. Antes disso, precisamos achar o fator integrante , que é dado da seguinte forma:
Passo 2
Agora que já sabemos o valor integrante, basta multiplicar toda a equação (i) por . Em que ficará assim:
Agora, para encontrar a equação final contendo a variável y em função de t basta seguir esse bizu abaixo:
, em que A é uma constante.
Mas, sabemos que , assim, substituímos na equação final descrita acima:
Porém, como diz o enunciado, quando g(t) = 0, temos:
Passo 3
Ou seja,
Logo, está provado.
Resposta
Ei, a resposta está no passo a passo :)